 CEO and founder Jensen Huang will host renowned AI pioneers Yoshua Bengio, Geoffrey Hinton and Yann LeCun at the company’s upcoming technology conference.
CEO and founder Jensen Huang will host renowned AI pioneers Yoshua Bengio, Geoffrey Hinton and Yann LeCun at the company’s upcoming technology conference.
Month: March 2021
 With highly performant software containers, pre-trained models, industry specific SDKs and Helm Charts, the content available on the catalog helps you simplify and accelerate your end-to-end workflows.
With highly performant software containers, pre-trained models, industry specific SDKs and Helm Charts, the content available on the catalog helps you simplify and accelerate your end-to-end workflows.
The NVIDIA NGC catalog is a hub for GPU-optimized deep learning, machine learning and high-performance computing (HPC) applications. With highly performant software containers, pre-trained models, industry specific SDKs and Helm Charts, the content available on the catalog helps you simplify and accelerate your end-to-end workflows.
The NVIDIA NGC team works closely with our internal and external partners to update the content in the catalog on a regular basis. Below are some of the highlights:
Artificial Intelligence
Jarvis AI Collections
NVIDIA announced the availability of Jarvis Beta 1.0. Jarvis is a fully accelerated application framework for building multimodal conversational AI services that use an end-to-end deep learning pipeline.
You can get started with the Jarvis AI services for various tasks ranging from speech recognition to question answering to intent detection and more – through the collections available on the NGC catalog.
Containers
- Our most popular deep learning frameworks for training and inference have been updated to the latest 21.02 version
- We also have added containers built by our partners
- Samsung SDS Brightics AI Accelerator for automatic and accelerating deep learning training
- Sony’s Neural Network Libraries, a deep learning framework that can be in research, development and production
Helm Charts
- NVIDIA GPU Operator has been updated to version 1.6.0 with added support for Red Hat OpenShift 4.7 and support for the R460 driver for datacenter NVIDIA GPUs. GPU Operator 1.5 was released in late January which added support for NVIDIA vGPU.
High Performance Computing
Containers
- The Quantum ESPRESSO container has also been updated to version 6.7. The latest version of our container delivers better performance with improvements related to CPU multithreading of FFTs and updated UCX settings.
- The NGC Pre-flight Check container is a light-weight tool that verifies that the container runtime is set up correctly for GPUs and InfiniBand. You can run this container prior to running your HPC or deep learning container on your system.
Additional Resources
- For those who are getting started with AI or need a head start with your use-case, we have built sample Jupyter Notebooks for both Image Segmentation and Recommender System to help you get started with these use-cases.

This is the first post in a series introducing time-series forecasting with torch. It does assume some prior experience with torch and/or deep learning. But as far as time series are concerned, it starts right from the beginning, using recurrent neural networks (GRU or LSTM) to predict how something develops in time.
In this post, we build a network that uses a sequence of observations to predict a value for the very next point in time. What if we’d like to forecast a sequence of values, corresponding to, say, a week or a month of measurements?
One thing we could do is feed back into the system the previously forecasted value; this is something we’ll try at the end of this post. Subsequent posts will explore other options, some of them involving significantly more complex architectures. It will be interesting to compare their performances; but the essential goal is to introduce some torch “recipes” that you can apply to your own data.
We start by examining the dataset used. It is a low-dimensional, but pretty polyvalent and complex one.
Time-series inspection
The vic_elec dataset, available through package tsibbledata, provides three years of half-hourly electricity demand for Victoria, Australia, augmented by same-resolution temperature information and a daily holiday indicator.
library(tidyverse) library(lubridate) library(tsibble) # Tidy Temporal Data Frames and Tools library(feasts) # Feature Extraction and Statistics for Time Series library(tsibbledata) # Diverse Datasets for 'tsibble' vic_elec %>% glimpse()
Rows: 52,608 Columns: 5 $ Time <dttm> 2012-01-01 00:00:00, 2012-01-01 00:30:00, 2012-01-01 01:00:00,… $ Demand <dbl> 4382.825, 4263.366, 4048.966, 3877.563, 4036.230, 3865.597, 369… $ Temperature <dbl> 21.40, 21.05, 20.70, 20.55, 20.40, 20.25, 20.10, 19.60, 19.10, … $ Date <date> 2012-01-01, 2012-01-01, 2012-01-01, 2012-01-01, 2012-01-01, 20… $ Holiday <lgl> TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRU…
Depending on what subset of variables is used, and whether and how data is temporally aggregated, these data may serve to illustrate a variety of different techniques. For example, in the third edition of Forecasting: Principles and Practice daily averages are used to teach quadratic regression with ARMA errors. In this first introductory post though, as well as in most of its successors, we’ll attempt to forecast Demand without relying on additional information, and we keep the original resolution.
To get an impression of how electricity demand varies over different timescales. Let’s inspect data for two months that nicely illustrate the U-shaped relationship between temperature and demand: January, 2014 and July, 2014.
First, here is July.
vic_elec_2014 <- vic_elec %>%
filter(year(Date) == 2014) %>%
select(-c(Date, Holiday)) %>%
mutate(Demand = scale(Demand), Temperature = scale(Temperature)) %>%
pivot_longer(-Time, names_to = "variable") %>%
update_tsibble(key = variable)
vic_elec_2014 %>% filter(month(Time) == 7) %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f")) +
theme_minimal()

(#fig:unnamed-chunk-3)Temperature and electricity demand (normalized). Victoria, Australia, 07/2014.
It’s winter; temperature fluctuates below average, while electricity demand is above average (heating). There is strong variation over the course of the day; we see troughs in the demand curve corresponding to ridges in the temperature graph, and vice versa. While diurnal variation dominates, there also is variation over the days of the week. Between weeks though, we don’t see much difference.
Compare this with the data for January:
vic_elec_2014 %>% filter(month(Time) == 1) %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f")) +
theme_minimal()
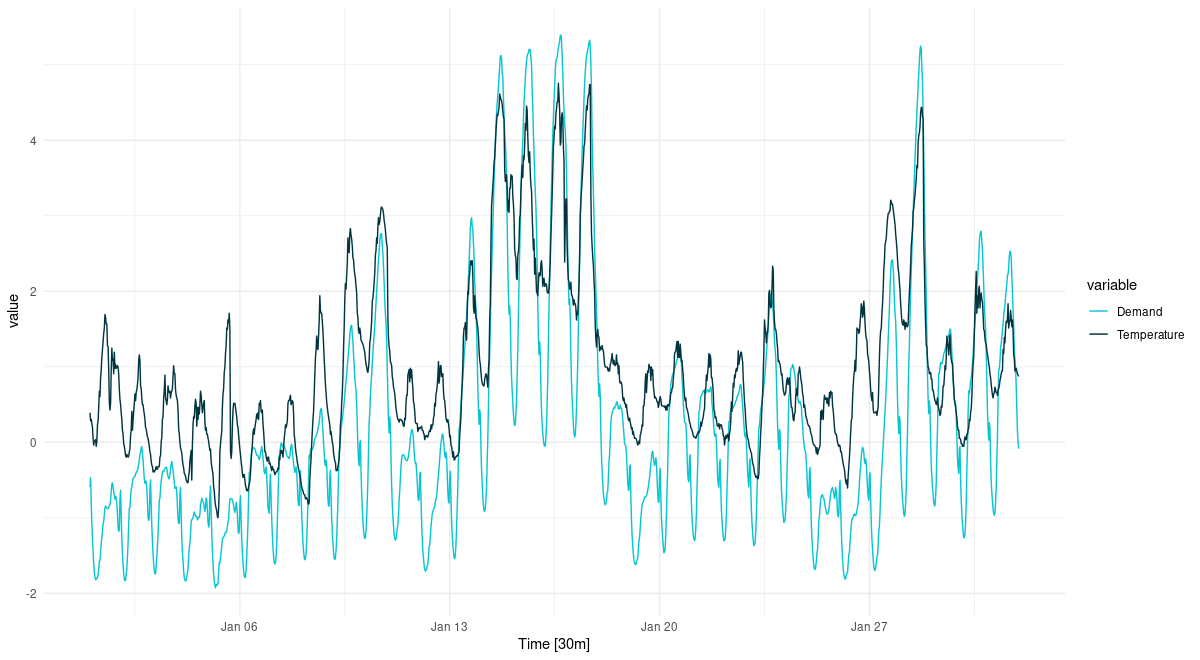
(#fig:unnamed-chunk-5)Temperature and electricity demand (normalized). Victoria, Australia, 01/2014.
We still see the strong circadian variation. We still see some day-of-week variation. But now it is high temperatures that cause elevated demand (cooling). Also, there are two periods of unusually high temperatures, accompanied by exceptional demand. We anticipate that in a univariate forecast, not taking into account temperature, this will be hard – or even, impossible – to forecast.
Let’s see a concise portrait of how Demand behaves using feasts::STL(). First, here is the decomposition for July:
vic_elec_2014 <- vic_elec %>% filter(year(Date) == 2014) %>% select(-c(Date, Holiday)) cmp <- vic_elec_2014 %>% filter(month(Time) == 7) %>% model(STL(Demand)) %>% components() cmp %>% autoplot()
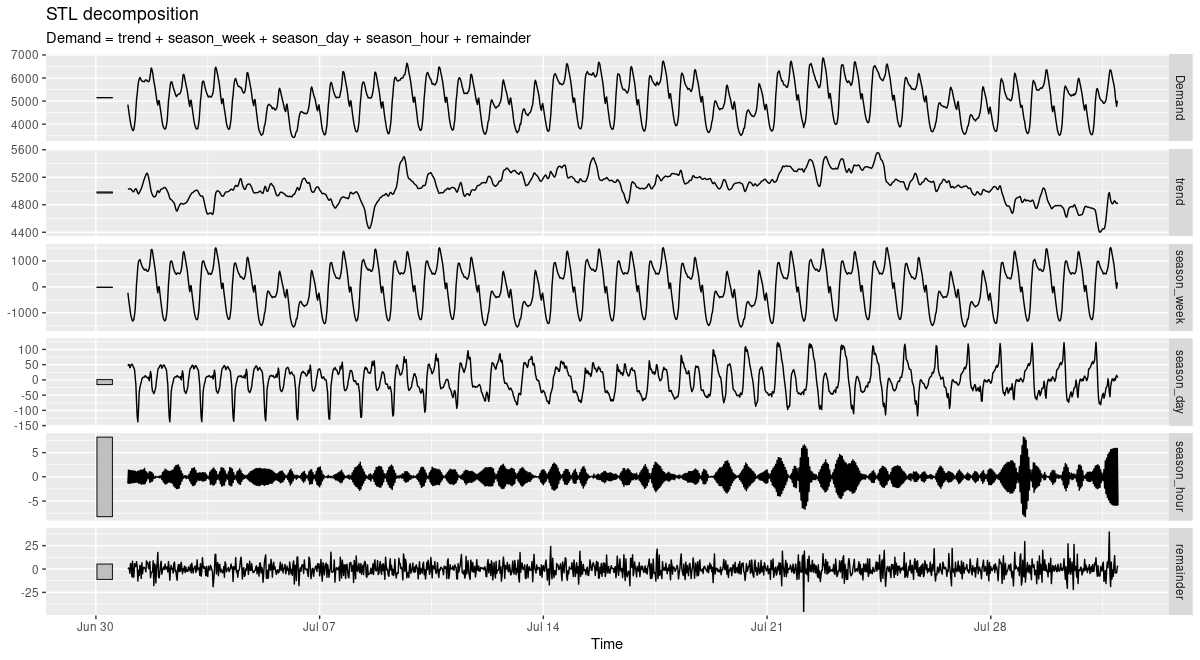
(#fig:unnamed-chunk-7)STL decomposition of electricity demand. Victoria, Australia, 07/2014.
And here, for January:
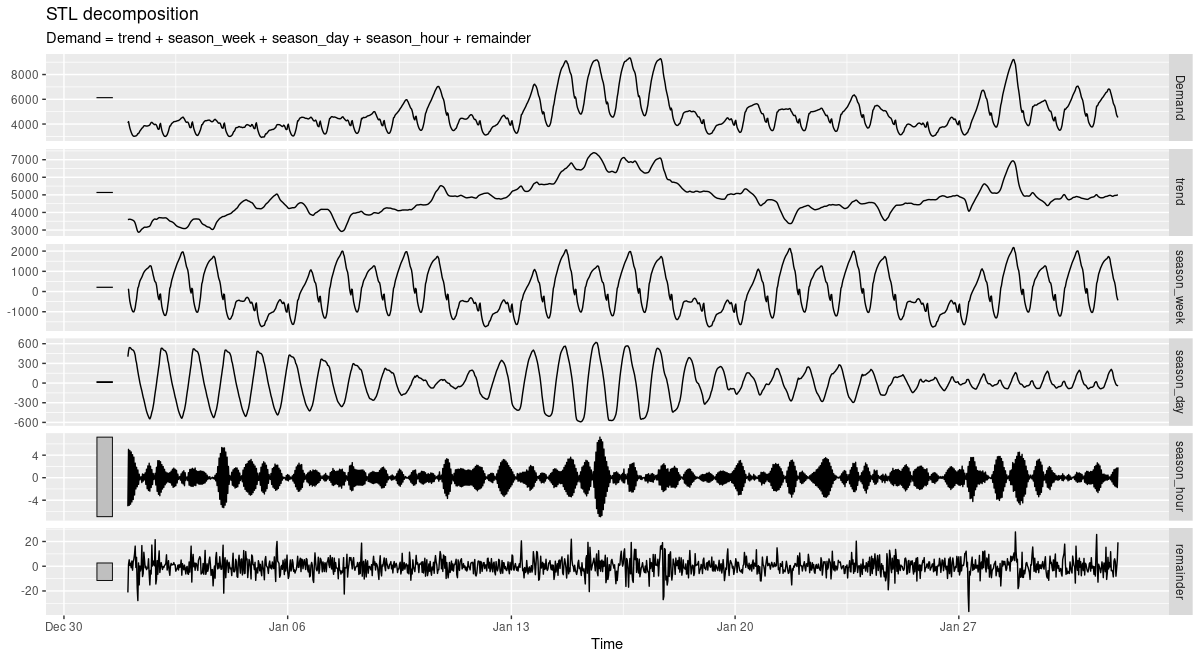
(#fig:unnamed-chunk-8)STL decomposition of electricity demand. Victoria, Australia, 01/2014.
Both nicely illustrate the strong circadian and weekly seasonalities (with diurnal variation substantially stronger in January). If we look closely, we can even see how the trend component is more influential in January than in July. This again hints at much stronger difficulties predicting the January than the July developments.
Now that we have an idea what awaits us, let’s begin by creating a torch dataset.
Data input
Here is what we intend to do. We want to start our journey into forecasting by using a sequence of observations to predict their immediate successor. In other words, the input (x) for each batch item is a vector, while the target (y) is a single value. The length of the input sequence, x, is parameterized as n_timesteps, the number of consecutive observations to extrapolate from.
The dataset will reflect this in its .getitem() method. When asked for the observations at index i, it will return tensors like so:
list(
x = self$x[start:end],
y = self$x[end+1]
)
where start:end is a vector of indices, of length n_timesteps, and end+1 is a single index.
Now, if the dataset just iterated over its input in order, advancing the index one at a time, these lines could simply read
list(
x = self$x[i:(i + self$n_timesteps - 1)],
y = self$x[self$n_timesteps + 1]
)
Since many sequences in the data are similar, we can reduce training time by making use of a fraction of the data in every epoch. This can be accomplished by (optionally) passing a sample_frac smaller than 1. In initialize(), a random set of start indices is prepared; .getitem() then just does what it normally does: look for the (x,y) pair at a given index.
Here is the complete dataset code:
elec_dataset <- dataset(
name = "elec_dataset",
initialize = function(x, n_timesteps, sample_frac = 1) {
self$n_timesteps <- n_timesteps
self$x <- torch_tensor((x - train_mean) / train_sd)
n <- length(self$x) - self$n_timesteps
self$starts <- sort(sample.int(
n = n,
size = n * sample_frac
))
},
.getitem = function(i) {
start <- self$starts[i]
end <- start + self$n_timesteps - 1
list(
x = self$x[start:end],
y = self$x[end + 1]
)
},
.length = function() {
length(self$starts)
}
)
You may have noticed that we normalize the data by globally defined train_mean and train_sd. We yet have to calculate those.
The way we split the data is straightforward. We use the whole of 2012 for training, and all of 2013 for validation. For testing, we take the “difficult” month of January, 2014. You are invited to compare testing results for July that same year, and compare performances.
vic_elec_get_year <- function(year, month = NULL) {
vic_elec %>%
filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else month) %>%
as_tibble() %>%
select(Demand)
}
elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix() # or 2014, 7, alternatively
train_mean <- mean(elec_train)
train_sd <- sd(elec_train)
Now, to instantiate a dataset, we still need to pick sequence length. From prior inspection, a week seems like a sensible choice.
n_timesteps <- 7 * 24 * 2 # days * hours * half-hours
Now we can go ahead and create a dataset for the training data. Let’s say we’ll make use of 50% of the data in each epoch:
train_ds <- elec_dataset(elec_train, n_timesteps, sample_frac = 0.5) length(train_ds)
8615
Quick check: Are the shapes correct?
train_ds[1]
$x
torch_tensor
-0.4141
-0.5541
[...] ### lines removed by me
0.8204
0.9399
... [the output was truncated (use n=-1 to disable)]
[ CPUFloatType{336,1} ]
$y
torch_tensor
-0.6771
[ CPUFloatType{1} ]
Yes: This is what we wanted to see. The input sequence has n_timesteps values in the first dimension, and a single one in the second, corresponding to the only feature present, Demand. As intended, the prediction tensor holds a single value, corresponding– as we know – to n_timesteps+1.
That takes care of a single input-output pair. As usual, batching is arranged for by torch’s dataloader class. We instantiate one for the training data, and immediately again verify the outcome:
batch_size <- 32 train_dl <- train_ds %>% dataloader(batch_size = batch_size, shuffle = TRUE) length(train_dl) b <- train_dl %>% dataloader_make_iter() %>% dataloader_next() b
$x
torch_tensor
(1,.,.) =
0.4805
0.3125
[...] ### lines removed by me
-1.1756
-0.9981
... [the output was truncated (use n=-1 to disable)]
[ CPUFloatType{32,336,1} ]
$y
torch_tensor
0.1890
0.5405
[...] ### lines removed by me
2.4015
0.7891
... [the output was truncated (use n=-1 to disable)]
[ CPUFloatType{32,1} ]
We see the added batch dimension in front, resulting in overall shape (batch_size, n_timesteps, num_features). This is the format expected by the model, or more precisely, by its initial RNN layer.
Before we go on, let’s quickly create datasets and dataloaders for validation and test data, as well.
valid_ds <- elec_dataset(elec_valid, n_timesteps, sample_frac = 0.5) valid_dl <- valid_ds %>% dataloader(batch_size = batch_size) test_ds <- elec_dataset(elec_test, n_timesteps) test_dl <- test_ds %>% dataloader(batch_size = 1)
Model
The model consists of an RNN – of type GRU or LSTM, as per the user’s choice – and an output layer. The RNN does most of the work; the single-neuron linear layer that outputs the prediction compresses its vector input to a single value.
Here, first, is the model definition.
model <- nn_module(
initialize = function(type, input_size, hidden_size, num_layers = 1, dropout = 0) {
self$type <- type
self$num_layers <- num_layers
self$rnn <- if (self$type == "gru") {
nn_gru(
input_size = input_size,
hidden_size = hidden_size,
num_layers = num_layers,
dropout = dropout,
batch_first = TRUE
)
} else {
nn_lstm(
input_size = input_size,
hidden_size = hidden_size,
num_layers = num_layers,
dropout = dropout,
batch_first = TRUE
)
}
self$output <- nn_linear(hidden_size, 1)
},
forward = function(x) {
# list of [output, hidden]
# we use the output, which is of size (batch_size, n_timesteps, hidden_size)
x <- self$rnn(x)[[1]]
# from the output, we only want the final timestep
# shape now is (batch_size, hidden_size)
x <- x[ , dim(x)[2], ]
# feed this to a single output neuron
# final shape then is (batch_size, 1)
x %>% self$output()
}
)
Most importantly, this is what happens in forward().
-
The RNN returns a list. The list holds two tensors, an output, and a synopsis of hidden states. We discard the state tensor, and keep the output only. The distinction between state and output, or rather, the way it is reflected in what a torch RNN returns, deserves to be inspected more closely. We’ll do that in a second.
x <- self$rnn(x)[[1]]
-
Of the output tensor, we’re interested in only the final time-step, though.
x <- x[ , dim(x)[2], ]
-
Only this one, thus, is passed to the output layer.
x %>% self$output()
-
Finally, the said output layer’s output is returned.
Now, a bit more on states vs. outputs. Consider Fig. 1, from Goodfellow, Bengio, and Courville (2016).
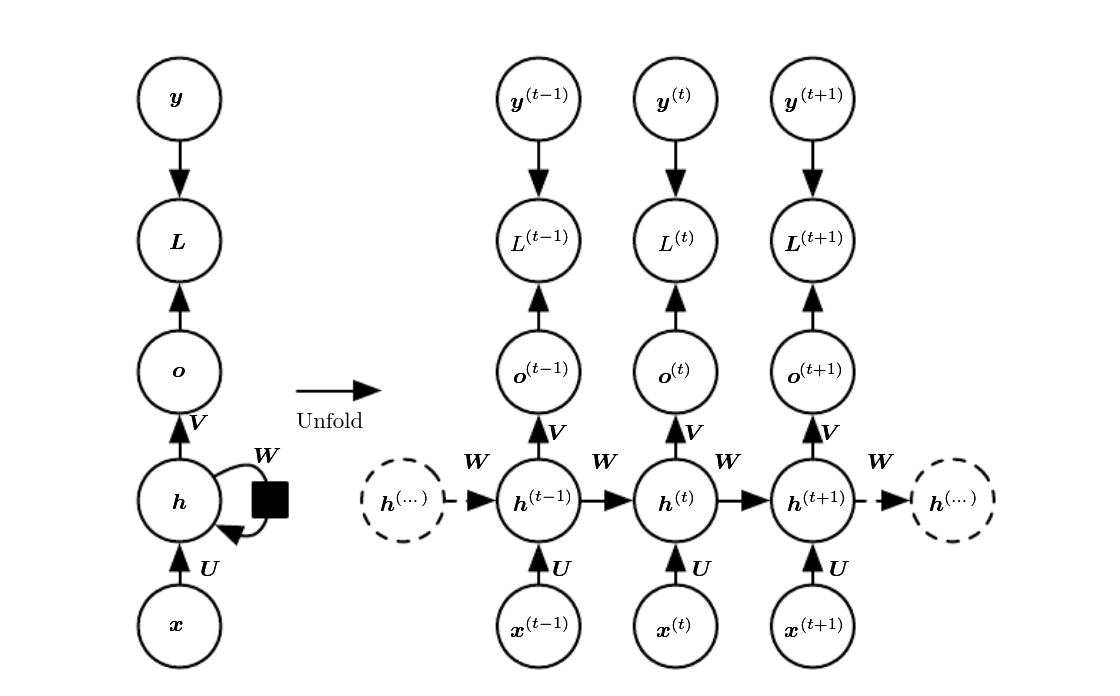
(#fig:unnamed-chunk-22)Source: Goodfellow et al., Deep learning. Chapter URL: https://www.deeplearningbook.org/contents/rnn.html.
Let’s pretend there are three time steps only, corresponding to (t-1), (t), and (t+1). The input sequence, accordingly, is composed of (x_{t-1}), (x_{t}), and (x_{t+1}).
At each (t), a hidden state is generated, and so is an output. Normally, if our goal is to predict (y_{t+2}), that is, the very next observation, we want to take into account the complete input sequence. Put differently, we want to have run through the complete machinery of state updates. The logical thing to do would thus be to choose (o_{t+1}), for either direct return from forward() or for further processing.
Indeed, return (o_{t+1}) is what a Keras LSTM or GRU would do by default.1 Not so its torch counterparts. In torch, the output tensor comprises all of (o). This is why, in step two above, we select the single time step we’re interested in – namely, the last one.
In later posts, we will make use of more than the last time step. Sometimes, we’ll use the sequence of hidden states (the (h)s) instead of the outputs (the (o)s). So you may feel like asking, what if we used (h_{t+1}) here instead of (o_{t+1})? The answer is: With a GRU, this would not make a difference, as those two are identical. With LSTM though, it would, as LSTM keeps a second, namely, the “cell”, state2.
On to initialize(). For ease of experimentation, we instantiate either a GRU or an LSTM based on user input. Two things are worth noting:
-
We pass batch_first = TRUE when creating the RNNs. This is required with torch RNNs when we want to consistently have batch items stacked in the first dimension. And we do want that; it is arguably less confusing than a change of dimension semantics for one sub-type of module.
-
num_layers can be used to build a stacked RNN, corresponding to what you’d get in Keras when chaining two GRUs/LSTMs (the first one created with return_sequences = TRUE). This parameter, too, we’ve included for quick experimentation.
Let’s instantiate a model for training. It will be a single-layer GRU with thirty-two units.
# training RNNs on the GPU currently prints a warning that may clutter
# the console
# see https://github.com/mlverse/torch/issues/461
# alternatively, use
# device <- "cpu"
device <- torch_device(if (cuda_is_available()) "cuda" else "cpu")
net <- model("gru", 1, 32)
net <- net$to(device = device)
Training
After all those RNN specifics, the training process is completely standard.
optimizer <- optim_adam(net$parameters, lr = 0.001)
num_epochs <- 30
train_batch <- function(b) {
optimizer$zero_grad()
output <- net(b$x$to(device = device))
target <- b$y$to(device = device)
loss <- nnf_mse_loss(output, target)
loss$backward()
optimizer$step()
loss$item()
}
valid_batch <- function(b) {
output <- net(b$x$to(device = device))
target <- b$y$to(device = device)
loss <- nnf_mse_loss(output, target)
loss$item()
}
for (epoch in 1:num_epochs) {
net$train()
train_loss <- c()
coro::loop(for (b in train_dl) {
loss <-train_batch(b)
train_loss <- c(train_loss, loss)
})
cat(sprintf("nEpoch %d, training: loss: %3.5f n", epoch, mean(train_loss)))
net$eval()
valid_loss <- c()
coro::loop(for (b in valid_dl) {
loss <- valid_batch(b)
valid_loss <- c(valid_loss, loss)
})
cat(sprintf("nEpoch %d, validation: loss: %3.5f n", epoch, mean(valid_loss)))
}
Epoch 1, training: loss: 0.21908 Epoch 1, validation: loss: 0.05125 Epoch 2, training: loss: 0.03245 Epoch 2, validation: loss: 0.03391 Epoch 3, training: loss: 0.02346 Epoch 3, validation: loss: 0.02321 Epoch 4, training: loss: 0.01823 Epoch 4, validation: loss: 0.01838 Epoch 5, training: loss: 0.01522 Epoch 5, validation: loss: 0.01560 Epoch 6, training: loss: 0.01315 Epoch 6, validation: loss: 0.01374 Epoch 7, training: loss: 0.01205 Epoch 7, validation: loss: 0.01200 Epoch 8, training: loss: 0.01155 Epoch 8, validation: loss: 0.01157 Epoch 9, training: loss: 0.01118 Epoch 9, validation: loss: 0.01096 Epoch 10, training: loss: 0.01070 Epoch 10, validation: loss: 0.01132 Epoch 11, training: loss: 0.01003 Epoch 11, validation: loss: 0.01150 Epoch 12, training: loss: 0.00943 Epoch 12, validation: loss: 0.01106 Epoch 13, training: loss: 0.00922 Epoch 13, validation: loss: 0.01069 Epoch 14, training: loss: 0.00862 Epoch 14, validation: loss: 0.01125 Epoch 15, training: loss: 0.00842 Epoch 15, validation: loss: 0.01095 Epoch 16, training: loss: 0.00820 Epoch 16, validation: loss: 0.00975 Epoch 17, training: loss: 0.00802 Epoch 17, validation: loss: 0.01120 Epoch 18, training: loss: 0.00781 Epoch 18, validation: loss: 0.00990 Epoch 19, training: loss: 0.00757 Epoch 19, validation: loss: 0.01017 Epoch 20, training: loss: 0.00735 Epoch 20, validation: loss: 0.00932 Epoch 21, training: loss: 0.00723 Epoch 21, validation: loss: 0.00901 Epoch 22, training: loss: 0.00708 Epoch 22, validation: loss: 0.00890 Epoch 23, training: loss: 0.00676 Epoch 23, validation: loss: 0.00914 Epoch 24, training: loss: 0.00666 Epoch 24, validation: loss: 0.00922 Epoch 25, training: loss: 0.00644 Epoch 25, validation: loss: 0.00869 Epoch 26, training: loss: 0.00620 Epoch 26, validation: loss: 0.00902 Epoch 27, training: loss: 0.00588 Epoch 27, validation: loss: 0.00896 Epoch 28, training: loss: 0.00563 Epoch 28, validation: loss: 0.00886 Epoch 29, training: loss: 0.00547 Epoch 29, validation: loss: 0.00895 Epoch 30, training: loss: 0.00523 Epoch 30, validation: loss: 0.00935
Loss decreases quickly, and we don’t seem to be overfitting on the validation set.
Numbers are pretty abstract, though. So, we’ll use the test set to see how the forecast actually looks.
Evaluation
Here is the forecast for January, 2014, thirty minutes at a time.
net$eval()
preds <- rep(NA, n_timesteps)
coro::loop(for (b in test_dl) {
output <- net(b$x$to(device = device))
preds <- c(preds, output %>% as.numeric())
})
vic_elec_jan_2014 <- vic_elec %>%
filter(year(Date) == 2014, month(Date) == 1) %>%
select(Demand)
preds_ts <- vic_elec_jan_2014 %>%
add_column(forecast = preds * train_sd + train_mean) %>%
pivot_longer(-Time) %>%
update_tsibble(key = name)
preds_ts %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f")) +
theme_minimal()
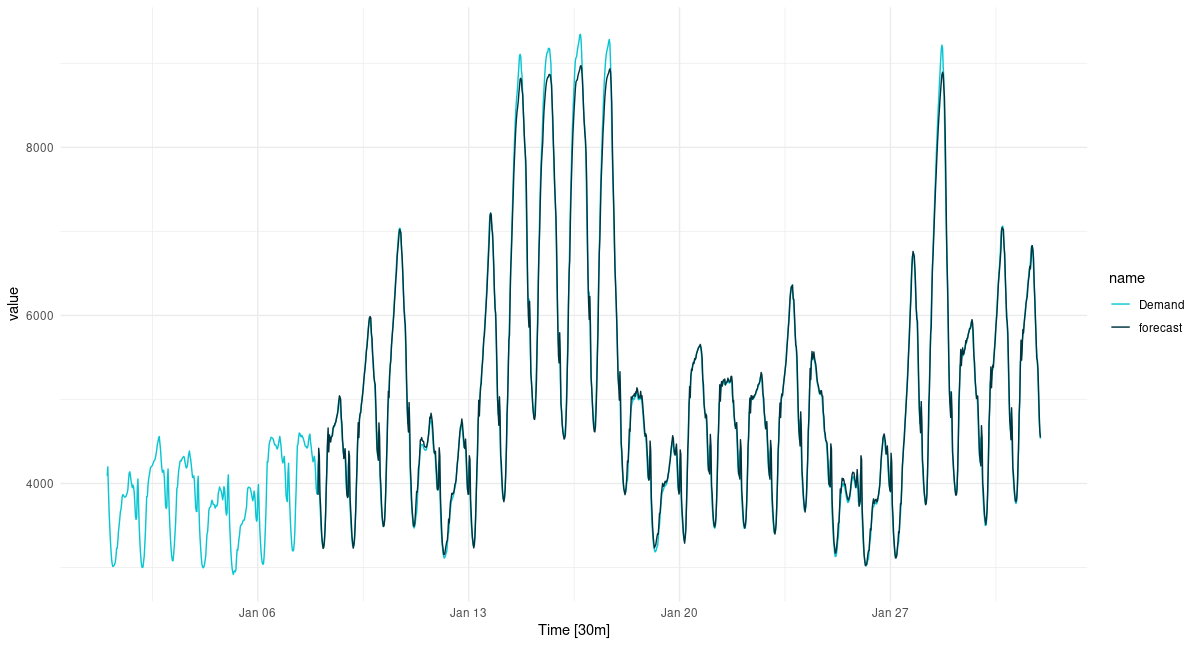
(#fig:unnamed-chunk-26)One-step-ahead predictions for January, 2014.
Overall, the forecast is excellent, but it is interesting to see how the forecast “regularizes” the most extreme peaks. This kind of “regression to the mean” will be seen much more strongly in later setups, when we try to forecast further into the future.
Can we use our current architecture for multi-step prediction? We can.
One thing we can do is feed back the current prediction, that is, append it to the input sequence as soon as it is available. Effectively thus, for each batch item, we obtain a sequence of predictions in a loop.
We’ll try to forecast 336 time steps, that is, a complete week.
n_forecast <- 2 * 24 * 7
test_preds <- vector(mode = "list", length = length(test_dl))
i <- 1
coro::loop(for (b in test_dl) {
input <- b$x
output <- net(input$to(device = device))
preds <- as.numeric(output)
for(j in 2:n_forecast) {
input <- torch_cat(list(input[ , 2:length(input), ], output$view(c(1, 1, 1))), dim = 2)
output <- net(input$to(device = device))
preds <- c(preds, as.numeric(output))
}
test_preds[[i]] <- preds
i <<- i + 1
})
For visualization, let’s pick three non-overlapping sequences.
test_pred1 <- test_preds[[1]]
test_pred1 <- c(rep(NA, n_timesteps), test_pred1, rep(NA, nrow(vic_elec_jan_2014) - n_timesteps - n_forecast))
test_pred2 <- test_preds[[408]]
test_pred2 <- c(rep(NA, n_timesteps + 407), test_pred2, rep(NA, nrow(vic_elec_jan_2014) - 407 - n_timesteps - n_forecast))
test_pred3 <- test_preds[[817]]
test_pred3 <- c(rep(NA, nrow(vic_elec_jan_2014) - n_forecast), test_pred3)
preds_ts <- vic_elec %>%
filter(year(Date) == 2014, month(Date) == 1) %>%
select(Demand) %>%
add_column(
iterative_ex_1 = test_pred1 * train_sd + train_mean,
iterative_ex_2 = test_pred2 * train_sd + train_mean,
iterative_ex_3 = test_pred3 * train_sd + train_mean) %>%
pivot_longer(-Time) %>%
update_tsibble(key = name)
preds_ts %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f", "#ffbf66", "#d46f4d")) +
theme_minimal()
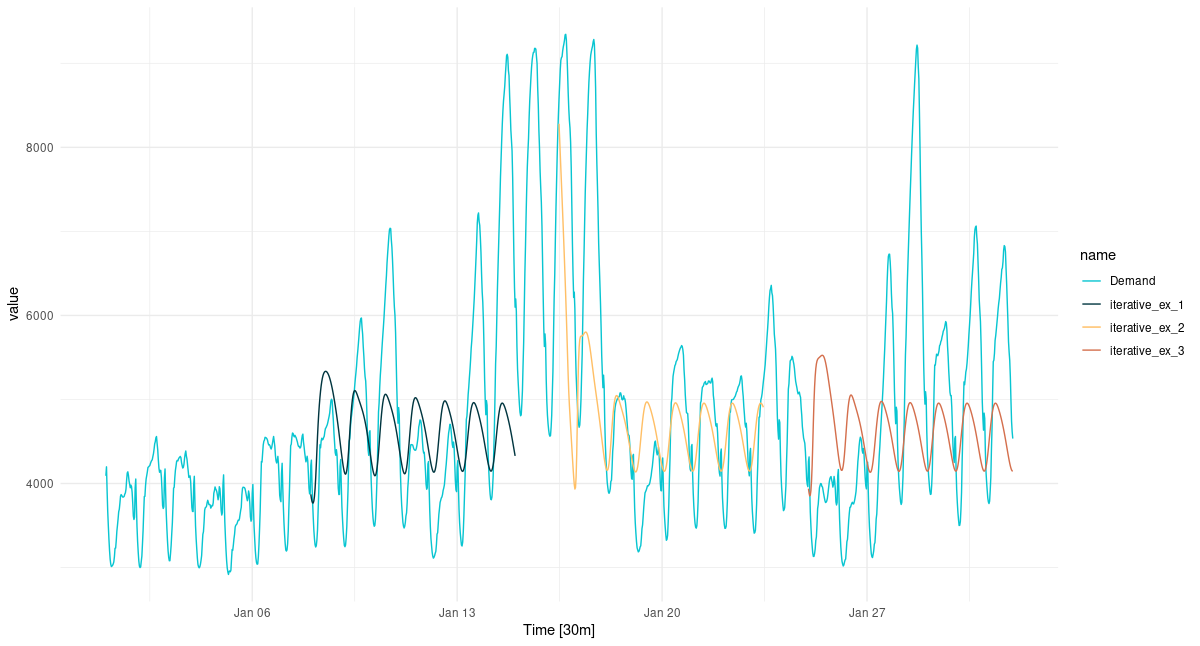
(#fig:unnamed-chunk-29)Multi-step predictions for January, 2014, obtained in a loop.
Even with this very basic forecasting technique, the diurnal rhythm is preserved, albeit in a strongly smoothed form. There even is an apparent day-of-week periodicity in the forecast. We do see, however, very strong regression to the mean, even in loop instances where the network was “primed” with a higher input sequence.
Conclusion
Hopefully this post provided a useful introduction to time series forecasting with torch. Evidently, we picked a challenging time series – challenging, that is, for at least two reasons:
-
To correctly factor in the trend, external information is needed: external information in form of a temperature forecast, which, “in reality”, would be easily obtainable.
-
In addition to the highly important trend component, the data are characterized by multiple levels..

We pick up where the first post in this series left us: confronting the task of multi-step time-series forecasting.
Our first attempt was a workaround of sorts. The model had been trained to deliver a single prediction, corresponding to the very next point in time. Thus, if we needed a longer forecast, all we could do is use that prediction and feed it back to the model, moving the input sequence by one value (from ([x_{t-n}, …, x_t]) to ([x_{t-n-1}, …, x_{t+1}]), say).
In contrast, the new model will be designed – and trained – to forecast a configurable number of observations at once. The architecture will still be basic – about as basic as possible, given the task – and thus, can serve as a baseline for later attempts.
Data input
We work with the same data as before, vic_elec from tsibbledata.
Compared to last time though, the dataset class has to change. While, previously, for each batch item the target (y) was a single value, it now is a vector, just like the input, x. And just like n_timesteps was (and still is) used to specify the length of the input sequence, there is now a second parameter, n_forecast, to configure target size.
In our example, n_timesteps and n_forecast are set to the same value, but there is no need for this to be the case. You could equally well train on week-long sequences and then forecast developments over a single day, or a month.
Apart from the fact that .getitem() now returns a vector for y as well as x, there is not much to be said about dataset creation. Here is the complete code to set up the data input pipeline:
n_timesteps <- 7 * 24 * 2
n_forecast <- 7 * 24 * 2
batch_size <- 32
vic_elec_get_year <- function(year, month = NULL) {
vic_elec %>%
filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else month) %>%
as_tibble() %>%
select(Demand)
}
elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix()
train_mean <- mean(elec_train)
train_sd <- sd(elec_train)
elec_dataset <- dataset(
name = "elec_dataset",
initialize = function(x, n_timesteps, n_forecast, sample_frac = 1) {
self$n_timesteps <- n_timesteps
self$n_forecast <- n_forecast
self$x <- torch_tensor((x - train_mean) / train_sd)
n <- length(self$x) - self$n_timesteps - self$n_forecast + 1
self$starts <- sort(sample.int(
n = n,
size = n * sample_frac
))
},
.getitem = function(i) {
start <- self$starts[i]
end <- start + self$n_timesteps - 1
pred_length <- self$n_forecast
list(
x = self$x[start:end],
y = self$x[(end + 1):(end + pred_length)]$squeeze(2)
)
},
.length = function() {
length(self$starts)
}
)
train_ds <- elec_dataset(elec_train, n_timesteps, n_forecast, sample_frac = 0.5)
train_dl <- train_ds %>% dataloader(batch_size = batch_size, shuffle = TRUE)
valid_ds <- elec_dataset(elec_valid, n_timesteps, n_forecast, sample_frac = 0.5)
valid_dl <- valid_ds %>% dataloader(batch_size = batch_size)
test_ds <- elec_dataset(elec_test, n_timesteps, n_forecast)
test_dl <- test_ds %>% dataloader(batch_size = 1)
Model
The model replaces the single linear layer that, in the previous post, had been tasked with outputting the final prediction, with a small network, complete with two linear layers and – optional – dropout.
In forward(), we first apply the RNN, and just like in the previous post, we make use of the outputs only; or more specifically, the output corresponding to the final time step. (See that previous post for a detailed discussion of what a torch RNN returns.)
model <- nn_module(
initialize = function(type, input_size, hidden_size, linear_size, output_size,
num_layers = 1, dropout = 0, linear_dropout = 0) {
self$type <- type
self$num_layers <- num_layers
self$linear_dropout <- linear_dropout
self$rnn <- if (self$type == "gru") {
nn_gru(
input_size = input_size,
hidden_size = hidden_size,
num_layers = num_layers,
dropout = dropout,
batch_first = TRUE
)
} else {
nn_lstm(
input_size = input_size,
hidden_size = hidden_size,
num_layers = num_layers,
dropout = dropout,
batch_first = TRUE
)
}
self$mlp <- nn_sequential(
nn_linear(hidden_size, linear_size),
nn_relu(),
nn_dropout(linear_dropout),
nn_linear(linear_size, output_size)
)
},
forward = function(x) {
x <- self$rnn(x)
x[[1]][ ,-1, ..] %>%
self$mlp()
}
)
For model instantiation, we now have an additional configuration parameter, related to the amount of dropout between the two linear layers.
net <- model( "gru", input_size = 1, hidden_size = 32, linear_size = 512, output_size = n_forecast, linear_dropout = 0 ) # training RNNs on the GPU currently prints a warning that may clutter # the console # see https://github.com/mlverse/torch/issues/461 # alternatively, use # device <- "cpu" device <- torch_device(if (cuda_is_available()) "cuda" else "cpu") net <- net$to(device = device)
Training
The training procedure is completely unchanged.
optimizer <- optim_adam(net$parameters, lr = 0.001)
num_epochs <- 30
train_batch <- function(b) {
optimizer$zero_grad()
output <- net(b$x$to(device = device))
target <- b$y$to(device = device)
loss <- nnf_mse_loss(output, target)
loss$backward()
optimizer$step()
loss$item()
}
valid_batch <- function(b) {
output <- net(b$x$to(device = device))
target <- b$y$to(device = device)
loss <- nnf_mse_loss(output, target)
loss$item()
}
for (epoch in 1:num_epochs) {
net$train()
train_loss <- c()
coro::loop(for (b in train_dl) {
loss <-train_batch(b)
train_loss <- c(train_loss, loss)
})
cat(sprintf("nEpoch %d, training: loss: %3.5f n", epoch, mean(train_loss)))
net$eval()
valid_loss <- c()
coro::loop(for (b in valid_dl) {
loss <- valid_batch(b)
valid_loss <- c(valid_loss, loss)
})
cat(sprintf("nEpoch %d, validation: loss: %3.5f n", epoch, mean(valid_loss)))
}
# Epoch 1, training: loss: 0.65737 # # Epoch 1, validation: loss: 0.54586 # # Epoch 2, training: loss: 0.43991 # # Epoch 2, validation: loss: 0.50588 # # Epoch 3, training: loss: 0.42161 # # Epoch 3, validation: loss: 0.50031 # # Epoch 4, training: loss: 0.41718 # # Epoch 4, validation: loss: 0.48703 # # Epoch 5, training: loss: 0.39498 # # Epoch 5, validation: loss: 0.49572 # # Epoch 6, training: loss: 0.38073 # # Epoch 6, validation: loss: 0.46813 # # Epoch 7, training: loss: 0.36472 # # Epoch 7, validation: loss: 0.44957 # # Epoch 8, training: loss: 0.35058 # # Epoch 8, validation: loss: 0.44440 # # Epoch 9, training: loss: 0.33880 # # Epoch 9, validation: loss: 0.41995 # # Epoch 10, training: loss: 0.32545 # # Epoch 10, validation: loss: 0.42021 # # Epoch 11, training: loss: 0.31347 # # Epoch 11, validation: loss: 0.39514 # # Epoch 12, training: loss: 0.29622 # # Epoch 12, validation: loss: 0.38146 # # Epoch 13, training: loss: 0.28006 # # Epoch 13, validation: loss: 0.37754 # # Epoch 14, training: loss: 0.27001 # # Epoch 14, validation: loss: 0.36636 # # Epoch 15, training: loss: 0.26191 # # Epoch 15, validation: loss: 0.35338 # # Epoch 16, training: loss: 0.25533 # # Epoch 16, validation: loss: 0.35453 # # Epoch 17, training: loss: 0.25085 # # Epoch 17, validation: loss: 0.34521 # # Epoch 18, training: loss: 0.24686 # # Epoch 18, validation: loss: 0.35094 # # Epoch 19, training: loss: 0.24159 # # Epoch 19, validation: loss: 0.33776 # # Epoch 20, training: loss: 0.23680 # # Epoch 20, validation: loss: 0.33974 # # Epoch 21, training: loss: 0.23070 # # Epoch 21, validation: loss: 0.34069 # # Epoch 22, training: loss: 0.22761 # # Epoch 22, validation: loss: 0.33724 # # Epoch 23, training: loss: 0.22390 # # Epoch 23, validation: loss: 0.34013 # # Epoch 24, training: loss: 0.22155 # # Epoch 24, validation: loss: 0.33460 # # Epoch 25, training: loss: 0.21820 # # Epoch 25, validation: loss: 0.33755 # # Epoch 26, training: loss: 0.22134 # # Epoch 26, validation: loss: 0.33678 # # Epoch 27, training: loss: 0.21061 # # Epoch 27, validation: loss: 0.33108 # # Epoch 28, training: loss: 0.20496 # # Epoch 28, validation: loss: 0.32769 # # Epoch 29, training: loss: 0.20223 # # Epoch 29, validation: loss: 0.32969 # # Epoch 30, training: loss: 0.20022 # # Epoch 30, validation: loss: 0.33331
From the way loss decreases on the training set, we conclude that, yes, the model is learning something. It probably would continue improving for quite some epochs still. We do, however, see less of an improvement on the validation set.
Naturally, now we’re curious about test-set predictions. (Remember, for testing we’re choosing the “particularly hard” month of January, 2014 – particularly hard because of a heatwave that resulted in exceptionally high demand.)
Evaluation
With no loop to be coded, evaluation now becomes pretty straightforward:
net$eval()
test_preds <- vector(mode = "list", length = length(test_dl))
i <- 1
coro::loop(for (b in test_dl) {
input <- b$x
output <- net(input$to(device = device))
preds <- as.numeric(output)
test_preds[[i]] <- preds
i <<- i + 1
})
vic_elec_jan_2014 <- vic_elec %>%
filter(year(Date) == 2014, month(Date) == 1)
test_pred1 <- test_preds[[1]]
test_pred1 <- c(rep(NA, n_timesteps), test_pred1, rep(NA, nrow(vic_elec_jan_2014) - n_timesteps - n_forecast))
test_pred2 <- test_preds[[408]]
test_pred2 <- c(rep(NA, n_timesteps + 407), test_pred2, rep(NA, nrow(vic_elec_jan_2014) - 407 - n_timesteps - n_forecast))
test_pred3 <- test_preds[[817]]
test_pred3 <- c(rep(NA, nrow(vic_elec_jan_2014) - n_forecast), test_pred3)
preds_ts <- vic_elec_jan_2014 %>%
select(Demand) %>%
add_column(
mlp_ex_1 = test_pred1 * train_sd + train_mean,
mlp_ex_2 = test_pred2 * train_sd + train_mean,
mlp_ex_3 = test_pred3 * train_sd + train_mean) %>%
pivot_longer(-Time) %>%
update_tsibble(key = name)
preds_ts %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f", "#ffbf66", "#d46f4d")) +
theme_minimal()

(#fig:unnamed-chunk-6)One-week-ahead predictions for January, 2014.
Compare this to the forecast obtained by feeding back predictions. The demand profiles over the day look a lot more realistic now. How about the phases of extreme demand? Evidently, these are not reflected in the forecast, not any more than in the “loop technique”. In fact, the forecast allows for interesting insights into this model’s personality: Apparently, it really likes fluctuating around the mean – “prime” it with inputs that oscillate around a significantly higher level, and it will quickly shift back to its comfort zone.
Discussion
Seeing how, above, we provided an option to use dropout inside the MLP, you may be wondering if this would help with forecasts on the test set. Turns out it did not, in my experiments. Maybe this is not so strange either: How, absent external cues (temperature), should the network know that high demand is coming up?
In our analysis, we can make an additional distinction. With the first week of predictions, what we see is a failure to anticipate something that could not reasonably have been anticipated (two, or two-and-a-half, say, days of exceptionally high demand). In the second, all the network would have had to do was stay at the current, elevated level. It will be interesting to see how this is handled by the architectures we discuss next.
Finally, an additional idea you may have had is – what if we used temperature as a second input variable? As a matter of fact, training performance indeed improved, but no performance impact was observed on the validation and test sets. Still, you may find the code useful – it is easily extended to datasets with more predictors. Therefore, we reproduce it in the appendix.
Thanks for reading!
Appendix
# Data input code modified to accommodate two predictors
n_timesteps <- 7 * 24 * 2
n_forecast <- 7 * 24 * 2
vic_elec_get_year <- function(year, month = NULL) {
vic_elec %>%
filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else month) %>%
as_tibble() %>%
select(Demand, Temperature)
}
elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix()
train_mean_demand <- mean(elec_train[ , 1])
train_sd_demand <- sd(elec_train[ , 1])
train_mean_temp <- mean(elec_train[ , 2])
train_sd_temp <- sd(elec_train[ , 2])
elec_dataset <- dataset(
name = "elec_dataset",
initialize = function(data, n_timesteps, n_forecast, sample_frac = 1) {
demand <- (data[ , 1] - train_mean_demand) / train_sd_demand
temp <- (data[ , 2] - train_mean_temp) / train_sd_temp
self$x <- cbind(demand, temp) %>% torch_tensor()
self$n_timesteps <- n_timesteps
self$n_forecast <- n_forecast
n <- nrow(self$x) - self$n_timesteps - self$n_forecast + 1
self$starts <- sort(sample.int(
n = n,
size = n * sample_frac
))
},
.getitem = function(i) {
start <- self$starts[i]
end <- start + self$n_timesteps - 1
pred_length <- self$n_forecast
list(
x = self$x[start:end, ],
y = self$x[(end + 1):(end + pred_length), 1]
)
},
.length = function() {
length(self$starts)
}
)
### rest identical to single-predictor code above
Photo by Monica Bourgeau on Unsplash
This is the first post in a series introducing time-series forecasting with torch. It does assume some prior experience with torch and/or deep learning. But as far as time series are concerned, it starts right from the beginning, using recurrent neural networks (GRU or LSTM) to predict how something develops in time.
In this post, we build a network that uses a sequence of observations to predict a value for the very next point in time. What if we’d like to forecast a sequence of values, corresponding to, say, a week or a month of measurements?
One thing we could do is feed back into the system the previously forecasted value; this is something we’ll try at the end of this post. Subsequent posts will explore other options, some of them involving significantly more complex architectures. It will be interesting to compare their performances; but the essential goal is to introduce some torch “recipes” that you can apply to your own data.
We start by examining the dataset used. It is a low-dimensional, but pretty polyvalent and complex one.
Time-series inspection
The vic_elec dataset, available through package tsibbledata, provides three years of half-hourly electricity demand for Victoria, Australia, augmented by same-resolution temperature information and a daily holiday indicator.
library(tidyverse) library(lubridate) library(tsibble) # Tidy Temporal Data Frames and Tools library(feasts) # Feature Extraction and Statistics for Time Series library(tsibbledata) # Diverse Datasets for 'tsibble' vic_elec %>% glimpse()
Rows: 52,608 Columns: 5 $ Time <dttm> 2012-01-01 00:00:00, 2012-01-01 00:30:00, 2012-01-01 01:00:00,… $ Demand <dbl> 4382.825, 4263.366, 4048.966, 3877.563, 4036.230, 3865.597, 369… $ Temperature <dbl> 21.40, 21.05, 20.70, 20.55, 20.40, 20.25, 20.10, 19.60, 19.10, … $ Date <date> 2012-01-01, 2012-01-01, 2012-01-01, 2012-01-01, 2012-01-01, 20… $ Holiday <lgl> TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRUE, TRU…
Depending on what subset of variables is used, and whether and how data is temporally aggregated, these data may serve to illustrate a variety of different techniques. For example, in the third edition of Forecasting: Principles and Practice daily averages are used to teach quadratic regression with ARMA errors. In this first introductory post though, as well as in most of its successors, we’ll attempt to forecast Demand without relying on additional information, and we keep the original resolution.
To get an impression of how electricity demand varies over different timescales. Let’s inspect data for two months that nicely illustrate the U-shaped relationship between temperature and demand: January, 2014 and July, 2014.
First, here is July.
vic_elec_2014 <- vic_elec %>%
filter(year(Date) == 2014) %>%
select(-c(Date, Holiday)) %>%
mutate(Demand = scale(Demand), Temperature = scale(Temperature)) %>%
pivot_longer(-Time, names_to = "variable") %>%
update_tsibble(key = variable)
vic_elec_2014 %>% filter(month(Time) == 7) %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f")) +
theme_minimal()

(#fig:unnamed-chunk-3)Temperature and electricity demand (normalized). Victoria, Australia, 07/2014.
It’s winter; temperature fluctuates below average, while electricity demand is above average (heating). There is strong variation over the course of the day; we see troughs in the demand curve corresponding to ridges in the temperature graph, and vice versa. While diurnal variation dominates, there also is variation over the days of the week. Between weeks though, we don’t see much difference.
Compare this with the data for January:
vic_elec_2014 %>% filter(month(Time) == 1) %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f")) +
theme_minimal()

(#fig:unnamed-chunk-5)Temperature and electricity demand (normalized). Victoria, Australia, 01/2014.
We still see the strong circadian variation. We still see some day-of-week variation. But now it is high temperatures that cause elevated demand (cooling). Also, there are two periods of unusually high temperatures, accompanied by exceptional demand. We anticipate that in a univariate forecast, not taking into account temperature, this will be hard – or even, impossible – to forecast.
Let’s see a concise portrait of how Demand behaves using feasts::STL(). First, here is the decomposition for July:
vic_elec_2014 <- vic_elec %>% filter(year(Date) == 2014) %>% select(-c(Date, Holiday)) cmp <- vic_elec_2014 %>% filter(month(Time) == 7) %>% model(STL(Demand)) %>% components() cmp %>% autoplot()

(#fig:unnamed-chunk-7)STL decomposition of electricity demand. Victoria, Australia, 07/2014.
And here, for January:

(#fig:unnamed-chunk-8)STL decomposition of electricity demand. Victoria, Australia, 01/2014.
Both nicely illustrate the strong circadian and weekly seasonalities (with diurnal variation substantially stronger in January). If we look closely, we can even see how the trend component is more influential in January than in July. This again hints at much stronger difficulties predicting the January than the July developments.
Now that we have an idea what awaits us, let’s begin by creating a torch dataset.
Data input
Here is what we intend to do. We want to start our journey into forecasting by using a sequence of observations to predict their immediate successor. In other words, the input (x) for each batch item is a vector, while the target (y) is a single value. The length of the input sequence, x, is parameterized as n_timesteps, the number of consecutive observations to extrapolate from.
The dataset will reflect this in its .getitem() method. When asked for the observations at index i, it will return tensors like so:
list(
x = self$x[start:end],
y = self$x[end+1]
)
where start:end is a vector of indices, of length n_timesteps, and end+1 is a single index.
Now, if the dataset just iterated over its input in order, advancing the index one at a time, these lines could simply read
list(
x = self$x[i:(i + self$n_timesteps - 1)],
y = self$x[self$n_timesteps + 1]
)
Since many sequences in the data are similar, we can reduce training time by making use of a fraction of the data in every epoch. This can be accomplished by (optionally) passing a sample_frac smaller than 1. In initialize(), a random set of start indices is prepared; .getitem() then just does what it normally does: look for the (x,y) pair at a given index.
Here is the complete dataset code:
elec_dataset <- dataset(
name = "elec_dataset",
initialize = function(x, n_timesteps, sample_frac = 1) {
self$n_timesteps <- n_timesteps
self$x <- torch_tensor((x - train_mean) / train_sd)
n <- length(self$x) - self$n_timesteps
self$starts <- sort(sample.int(
n = n,
size = n * sample_frac
))
},
.getitem = function(i) {
start <- self$starts[i]
end <- start + self$n_timesteps - 1
list(
x = self$x[start:end],
y = self$x[end + 1]
)
},
.length = function() {
length(self$starts)
}
)
You may have noticed that we normalize the data by globally defined train_mean and train_sd. We yet have to calculate those.
The way we split the data is straightforward. We use the whole of 2012 for training, and all of 2013 for validation. For testing, we take the “difficult” month of January, 2014. You are invited to compare testing results for July that same year, and compare performances.
vic_elec_get_year <- function(year, month = NULL) {
vic_elec %>%
filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else month) %>%
as_tibble() %>%
select(Demand)
}
elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix() # or 2014, 7, alternatively
train_mean <- mean(elec_train)
train_sd <- sd(elec_train)
Now, to instantiate a dataset, we still need to pick sequence length. From prior inspection, a week seems like a sensible choice.
n_timesteps <- 7 * 24 * 2 # days * hours * half-hours
Now we can go ahead and create a dataset for the training data. Let’s say we’ll make use of 50% of the data in each epoch:
train_ds <- elec_dataset(elec_train, n_timesteps, sample_frac = 0.5) length(train_ds)
8615
Quick check: Are the shapes correct?
train_ds[1]
$x
torch_tensor
-0.4141
-0.5541
[...] ### lines removed by me
0.8204
0.9399
... [the output was truncated (use n=-1 to disable)]
[ CPUFloatType{336,1} ]
$y
torch_tensor
-0.6771
[ CPUFloatType{1} ]
Yes: This is what we wanted to see. The input sequence has n_timesteps values in the first dimension, and a single one in the second, corresponding to the only feature present, Demand. As intended, the prediction tensor holds a single value, corresponding– as we know – to n_timesteps+1.
That takes care of a single input-output pair. As usual, batching is arranged for by torch’s dataloader class. We instantiate one for the training data, and immediately again verify the outcome:
batch_size <- 32 train_dl <- train_ds %>% dataloader(batch_size = batch_size, shuffle = TRUE) length(train_dl) b <- train_dl %>% dataloader_make_iter() %>% dataloader_next() b
$x
torch_tensor
(1,.,.) =
0.4805
0.3125
[...] ### lines removed by me
-1.1756
-0.9981
... [the output was truncated (use n=-1 to disable)]
[ CPUFloatType{32,336,1} ]
$y
torch_tensor
0.1890
0.5405
[...] ### lines removed by me
2.4015
0.7891
... [the output was truncated (use n=-1 to disable)]
[ CPUFloatType{32,1} ]
We see the added batch dimension in front, resulting in overall shape (batch_size, n_timesteps, num_features). This is the format expected by the model, or more precisely, by its initial RNN layer.
Before we go on, let’s quickly create datasets and dataloaders for validation and test data, as well.
valid_ds <- elec_dataset(elec_valid, n_timesteps, sample_frac = 0.5) valid_dl <- valid_ds %>% dataloader(batch_size = batch_size) test_ds <- elec_dataset(elec_test, n_timesteps) test_dl <- test_ds %>% dataloader(batch_size = 1)
Model
The model consists of an RNN – of type GRU or LSTM, as per the user’s choice – and an output layer. The RNN does most of the work; the single-neuron linear layer that outputs the prediction compresses its vector input to a single value.
Here, first, is the model definition.
model <- nn_module(
initialize = function(type, input_size, hidden_size, num_layers = 1, dropout = 0) {
self$type <- type
self$num_layers <- num_layers
self$rnn <- if (self$type == "gru") {
nn_gru(
input_size = input_size,
hidden_size = hidden_size,
num_layers = num_layers,
dropout = dropout,
batch_first = TRUE
)
} else {
nn_lstm(
input_size = input_size,
hidden_size = hidden_size,
num_layers = num_layers,
dropout = dropout,
batch_first = TRUE
)
}
self$output <- nn_linear(hidden_size, 1)
},
forward = function(x) {
# list of [output, hidden]
# we use the output, which is of size (batch_size, n_timesteps, hidden_size)
x <- self$rnn(x)[[1]]
# from the output, we only want the final timestep
# shape now is (batch_size, hidden_size)
x <- x[ , dim(x)[2], ]
# feed this to a single output neuron
# final shape then is (batch_size, 1)
x %>% self$output()
}
)
Most importantly, this is what happens in forward().
-
The RNN returns a list. The list holds two tensors, an output, and a synopsis of hidden states. We discard the state tensor, and keep the output only. The distinction between state and output, or rather, the way it is reflected in what a torch RNN returns, deserves to be inspected more closely. We’ll do that in a second.
x <- self$rnn(x)[[1]]
-
Of the output tensor, we’re interested in only the final time-step, though.
x <- x[ , dim(x)[2], ]
-
Only this one, thus, is passed to the output layer.
x %>% self$output()
-
Finally, the said output layer’s output is returned.
Now, a bit more on states vs. outputs. Consider Fig. 1, from Goodfellow, Bengio, and Courville (2016).

(#fig:unnamed-chunk-22)Source: Goodfellow et al., Deep learning. Chapter URL: https://www.deeplearningbook.org/contents/rnn.html.
Let’s pretend there are three time steps only, corresponding to (t-1), (t), and (t+1). The input sequence, accordingly, is composed of (x_{t-1}), (x_{t}), and (x_{t+1}).
At each (t), a hidden state is generated, and so is an output. Normally, if our goal is to predict (y_{t+2}), that is, the very next observation, we want to take into account the complete input sequence. Put differently, we want to have run through the complete machinery of state updates. The logical thing to do would thus be to choose (o_{t+1}), for either direct return from forward() or for further processing.
Indeed, return (o_{t+1}) is what a Keras LSTM or GRU would do by default.1 Not so its torch counterparts. In torch, the output tensor comprises all of (o). This is why, in step two above, we select the single time step we’re interested in – namely, the last one.
In later posts, we will make use of more than the last time step. Sometimes, we’ll use the sequence of hidden states (the (h)s) instead of the outputs (the (o)s). So you may feel like asking, what if we used (h_{t+1}) here instead of (o_{t+1})? The answer is: With a GRU, this would not make a difference, as those two are identical. With LSTM though, it would, as LSTM keeps a second, namely, the “cell”, state2.
On to initialize(). For ease of experimentation, we instantiate either a GRU or an LSTM based on user input. Two things are worth noting:
-
We pass batch_first = TRUE when creating the RNNs. This is required with torch RNNs when we want to consistently have batch items stacked in the first dimension. And we do want that; it is arguably less confusing than a change of dimension semantics for one sub-type of module.
-
num_layers can be used to build a stacked RNN, corresponding to what you’d get in Keras when chaining two GRUs/LSTMs (the first one created with return_sequences = TRUE). This parameter, too, we’ve included for quick experimentation.
Let’s instantiate a model for training. It will be a single-layer GRU with thirty-two units.
# training RNNs on the GPU currently prints a warning that may clutter
# the console
# see https://github.com/mlverse/torch/issues/461
# alternatively, use
# device <- "cpu"
device <- torch_device(if (cuda_is_available()) "cuda" else "cpu")
net <- model("gru", 1, 32)
net <- net$to(device = device)
Training
After all those RNN specifics, the training process is completely standard.
optimizer <- optim_adam(net$parameters, lr = 0.001)
num_epochs <- 30
train_batch <- function(b) {
optimizer$zero_grad()
output <- net(b$x$to(device = device))
target <- b$y$to(device = device)
loss <- nnf_mse_loss(output, target)
loss$backward()
optimizer$step()
loss$item()
}
valid_batch <- function(b) {
output <- net(b$x$to(device = device))
target <- b$y$to(device = device)
loss <- nnf_mse_loss(output, target)
loss$item()
}
for (epoch in 1:num_epochs) {
net$train()
train_loss <- c()
coro::loop(for (b in train_dl) {
loss <-train_batch(b)
train_loss <- c(train_loss, loss)
})
cat(sprintf("nEpoch %d, training: loss: %3.5f n", epoch, mean(train_loss)))
net$eval()
valid_loss <- c()
coro::loop(for (b in valid_dl) {
loss <- valid_batch(b)
valid_loss <- c(valid_loss, loss)
})
cat(sprintf("nEpoch %d, validation: loss: %3.5f n", epoch, mean(valid_loss)))
}
Epoch 1, training: loss: 0.21908 Epoch 1, validation: loss: 0.05125 Epoch 2, training: loss: 0.03245 Epoch 2, validation: loss: 0.03391 Epoch 3, training: loss: 0.02346 Epoch 3, validation: loss: 0.02321 Epoch 4, training: loss: 0.01823 Epoch 4, validation: loss: 0.01838 Epoch 5, training: loss: 0.01522 Epoch 5, validation: loss: 0.01560 Epoch 6, training: loss: 0.01315 Epoch 6, validation: loss: 0.01374 Epoch 7, training: loss: 0.01205 Epoch 7, validation: loss: 0.01200 Epoch 8, training: loss: 0.01155 Epoch 8, validation: loss: 0.01157 Epoch 9, training: loss: 0.01118 Epoch 9, validation: loss: 0.01096 Epoch 10, training: loss: 0.01070 Epoch 10, validation: loss: 0.01132 Epoch 11, training: loss: 0.01003 Epoch 11, validation: loss: 0.01150 Epoch 12, training: loss: 0.00943 Epoch 12, validation: loss: 0.01106 Epoch 13, training: loss: 0.00922 Epoch 13, validation: loss: 0.01069 Epoch 14, training: loss: 0.00862 Epoch 14, validation: loss: 0.01125 Epoch 15, training: loss: 0.00842 Epoch 15, validation: loss: 0.01095 Epoch 16, training: loss: 0.00820 Epoch 16, validation: loss: 0.00975 Epoch 17, training: loss: 0.00802 Epoch 17, validation: loss: 0.01120 Epoch 18, training: loss: 0.00781 Epoch 18, validation: loss: 0.00990 Epoch 19, training: loss: 0.00757 Epoch 19, validation: loss: 0.01017 Epoch 20, training: loss: 0.00735 Epoch 20, validation: loss: 0.00932 Epoch 21, training: loss: 0.00723 Epoch 21, validation: loss: 0.00901 Epoch 22, training: loss: 0.00708 Epoch 22, validation: loss: 0.00890 Epoch 23, training: loss: 0.00676 Epoch 23, validation: loss: 0.00914 Epoch 24, training: loss: 0.00666 Epoch 24, validation: loss: 0.00922 Epoch 25, training: loss: 0.00644 Epoch 25, validation: loss: 0.00869 Epoch 26, training: loss: 0.00620 Epoch 26, validation: loss: 0.00902 Epoch 27, training: loss: 0.00588 Epoch 27, validation: loss: 0.00896 Epoch 28, training: loss: 0.00563 Epoch 28, validation: loss: 0.00886 Epoch 29, training: loss: 0.00547 Epoch 29, validation: loss: 0.00895 Epoch 30, training: loss: 0.00523 Epoch 30, validation: loss: 0.00935
Loss decreases quickly, and we don’t seem to be overfitting on the validation set.
Numbers are pretty abstract, though. So, we’ll use the test set to see how the forecast actually looks.
Evaluation
Here is the forecast for January, 2014, thirty minutes at a time.
net$eval()
preds <- rep(NA, n_timesteps)
coro::loop(for (b in test_dl) {
output <- net(b$x$to(device = device))
preds <- c(preds, output %>% as.numeric())
})
vic_elec_jan_2014 <- vic_elec %>%
filter(year(Date) == 2014, month(Date) == 1) %>%
select(Demand)
preds_ts <- vic_elec_jan_2014 %>%
add_column(forecast = preds * train_sd + train_mean) %>%
pivot_longer(-Time) %>%
update_tsibble(key = name)
preds_ts %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f")) +
theme_minimal()

(#fig:unnamed-chunk-26)One-step-ahead predictions for January, 2014.
Overall, the forecast is excellent, but it is interesting to see how the forecast “regularizes” the most extreme peaks. This kind of “regression to the mean” will be seen much more strongly in later setups, when we try to forecast further into the future.
Can we use our current architecture for multi-step prediction? We can.
One thing we can do is feed back the current prediction, that is, append it to the input sequence as soon as it is available. Effectively thus, for each batch item, we obtain a sequence of predictions in a loop.
We’ll try to forecast 336 time steps, that is, a complete week.
n_forecast <- 2 * 24 * 7
test_preds <- vector(mode = "list", length = length(test_dl))
i <- 1
coro::loop(for (b in test_dl) {
input <- b$x
output <- net(input$to(device = device))
preds <- as.numeric(output)
for(j in 2:n_forecast) {
input <- torch_cat(list(input[ , 2:length(input), ], output$view(c(1, 1, 1))), dim = 2)
output <- net(input$to(device = device))
preds <- c(preds, as.numeric(output))
}
test_preds[[i]] <- preds
i <<- i + 1
})
For visualization, let’s pick three non-overlapping sequences.
test_pred1 <- test_preds[[1]]
test_pred1 <- c(rep(NA, n_timesteps), test_pred1, rep(NA, nrow(vic_elec_jan_2014) - n_timesteps - n_forecast))
test_pred2 <- test_preds[[408]]
test_pred2 <- c(rep(NA, n_timesteps + 407), test_pred2, rep(NA, nrow(vic_elec_jan_2014) - 407 - n_timesteps - n_forecast))
test_pred3 <- test_preds[[817]]
test_pred3 <- c(rep(NA, nrow(vic_elec_jan_2014) - n_forecast), test_pred3)
preds_ts <- vic_elec %>%
filter(year(Date) == 2014, month(Date) == 1) %>%
select(Demand) %>%
add_column(
iterative_ex_1 = test_pred1 * train_sd + train_mean,
iterative_ex_2 = test_pred2 * train_sd + train_mean,
iterative_ex_3 = test_pred3 * train_sd + train_mean) %>%
pivot_longer(-Time) %>%
update_tsibble(key = name)
preds_ts %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f", "#ffbf66", "#d46f4d")) +
theme_minimal()

(#fig:unnamed-chunk-29)Multi-step predictions for January, 2014, obtained in a loop.
Even with this very basic forecasting technique, the diurnal rhythm is preserved, albeit in a strongly smoothed form. There even is an apparent day-of-week periodicity in the forecast. We do see, however, very strong regression to the mean, even in loop instances where the network was “primed” with a higher input sequence.
Conclusion
Hopefully this post provided a useful introduction to time series forecasting with torch. Evidently, we picked a challenging time series – challenging, that is, for at least two reasons:
-
To correctly factor in the trend, external information is needed: external information in form of a temperature forecast, which, “in reality”, would be easily obtainable.
-
In addition to the highly important trend component, the data are characterized by multiple levels..
We pick up where the first post in this series left us: confronting the task of multi-step time-series forecasting.
Our first attempt was a workaround of sorts. The model had been trained to deliver a single prediction, corresponding to the very next point in time. Thus, if we needed a longer forecast, all we could do is use that prediction and feed it back to the model, moving the input sequence by one value (from ([x_{t-n}, …, x_t]) to ([x_{t-n-1}, …, x_{t+1}]), say).
In contrast, the new model will be designed – and trained – to forecast a configurable number of observations at once. The architecture will still be basic – about as basic as possible, given the task – and thus, can serve as a baseline for later attempts.
Data input
We work with the same data as before, vic_elec from tsibbledata.
Compared to last time though, the dataset class has to change. While, previously, for each batch item the target (y) was a single value, it now is a vector, just like the input, x. And just like n_timesteps was (and still is) used to specify the length of the input sequence, there is now a second parameter, n_forecast, to configure target size.
In our example, n_timesteps and n_forecast are set to the same value, but there is no need for this to be the case. You could equally well train on week-long sequences and then forecast developments over a single day, or a month.
Apart from the fact that .getitem() now returns a vector for y as well as x, there is not much to be said about dataset creation. Here is the complete code to set up the data input pipeline:
n_timesteps <- 7 * 24 * 2
n_forecast <- 7 * 24 * 2
batch_size <- 32
vic_elec_get_year <- function(year, month = NULL) {
vic_elec %>%
filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else month) %>%
as_tibble() %>%
select(Demand)
}
elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix()
train_mean <- mean(elec_train)
train_sd <- sd(elec_train)
elec_dataset <- dataset(
name = "elec_dataset",
initialize = function(x, n_timesteps, n_forecast, sample_frac = 1) {
self$n_timesteps <- n_timesteps
self$n_forecast <- n_forecast
self$x <- torch_tensor((x - train_mean) / train_sd)
n <- length(self$x) - self$n_timesteps - self$n_forecast + 1
self$starts <- sort(sample.int(
n = n,
size = n * sample_frac
))
},
.getitem = function(i) {
start <- self$starts[i]
end <- start + self$n_timesteps - 1
pred_length <- self$n_forecast
list(
x = self$x[start:end],
y = self$x[(end + 1):(end + pred_length)]$squeeze(2)
)
},
.length = function() {
length(self$starts)
}
)
train_ds <- elec_dataset(elec_train, n_timesteps, n_forecast, sample_frac = 0.5)
train_dl <- train_ds %>% dataloader(batch_size = batch_size, shuffle = TRUE)
valid_ds <- elec_dataset(elec_valid, n_timesteps, n_forecast, sample_frac = 0.5)
valid_dl <- valid_ds %>% dataloader(batch_size = batch_size)
test_ds <- elec_dataset(elec_test, n_timesteps, n_forecast)
test_dl <- test_ds %>% dataloader(batch_size = 1)
Model
The model replaces the single linear layer that, in the previous post, had been tasked with outputting the final prediction, with a small network, complete with two linear layers and – optional – dropout.
In forward(), we first apply the RNN, and just like in the previous post, we make use of the outputs only; or more specifically, the output corresponding to the final time step. (See that previous post for a detailed discussion of what a torch RNN returns.)
model <- nn_module(
initialize = function(type, input_size, hidden_size, linear_size, output_size,
num_layers = 1, dropout = 0, linear_dropout = 0) {
self$type <- type
self$num_layers <- num_layers
self$linear_dropout <- linear_dropout
self$rnn <- if (self$type == "gru") {
nn_gru(
input_size = input_size,
hidden_size = hidden_size,
num_layers = num_layers,
dropout = dropout,
batch_first = TRUE
)
} else {
nn_lstm(
input_size = input_size,
hidden_size = hidden_size,
num_layers = num_layers,
dropout = dropout,
batch_first = TRUE
)
}
self$mlp <- nn_sequential(
nn_linear(hidden_size, linear_size),
nn_relu(),
nn_dropout(linear_dropout),
nn_linear(linear_size, output_size)
)
},
forward = function(x) {
x <- self$rnn(x)
x[[1]][ ,-1, ..] %>%
self$mlp()
}
)
For model instantiation, we now have an additional configuration parameter, related to the amount of dropout between the two linear layers.
net <- model( "gru", input_size = 1, hidden_size = 32, linear_size = 512, output_size = n_forecast, linear_dropout = 0 ) # training RNNs on the GPU currently prints a warning that may clutter # the console # see https://github.com/mlverse/torch/issues/461 # alternatively, use # device <- "cpu" device <- torch_device(if (cuda_is_available()) "cuda" else "cpu") net <- net$to(device = device)
Training
The training procedure is completely unchanged.
optimizer <- optim_adam(net$parameters, lr = 0.001)
num_epochs <- 30
train_batch <- function(b) {
optimizer$zero_grad()
output <- net(b$x$to(device = device))
target <- b$y$to(device = device)
loss <- nnf_mse_loss(output, target)
loss$backward()
optimizer$step()
loss$item()
}
valid_batch <- function(b) {
output <- net(b$x$to(device = device))
target <- b$y$to(device = device)
loss <- nnf_mse_loss(output, target)
loss$item()
}
for (epoch in 1:num_epochs) {
net$train()
train_loss <- c()
coro::loop(for (b in train_dl) {
loss <-train_batch(b)
train_loss <- c(train_loss, loss)
})
cat(sprintf("nEpoch %d, training: loss: %3.5f n", epoch, mean(train_loss)))
net$eval()
valid_loss <- c()
coro::loop(for (b in valid_dl) {
loss <- valid_batch(b)
valid_loss <- c(valid_loss, loss)
})
cat(sprintf("nEpoch %d, validation: loss: %3.5f n", epoch, mean(valid_loss)))
}
# Epoch 1, training: loss: 0.65737 # # Epoch 1, validation: loss: 0.54586 # # Epoch 2, training: loss: 0.43991 # # Epoch 2, validation: loss: 0.50588 # # Epoch 3, training: loss: 0.42161 # # Epoch 3, validation: loss: 0.50031 # # Epoch 4, training: loss: 0.41718 # # Epoch 4, validation: loss: 0.48703 # # Epoch 5, training: loss: 0.39498 # # Epoch 5, validation: loss: 0.49572 # # Epoch 6, training: loss: 0.38073 # # Epoch 6, validation: loss: 0.46813 # # Epoch 7, training: loss: 0.36472 # # Epoch 7, validation: loss: 0.44957 # # Epoch 8, training: loss: 0.35058 # # Epoch 8, validation: loss: 0.44440 # # Epoch 9, training: loss: 0.33880 # # Epoch 9, validation: loss: 0.41995 # # Epoch 10, training: loss: 0.32545 # # Epoch 10, validation: loss: 0.42021 # # Epoch 11, training: loss: 0.31347 # # Epoch 11, validation: loss: 0.39514 # # Epoch 12, training: loss: 0.29622 # # Epoch 12, validation: loss: 0.38146 # # Epoch 13, training: loss: 0.28006 # # Epoch 13, validation: loss: 0.37754 # # Epoch 14, training: loss: 0.27001 # # Epoch 14, validation: loss: 0.36636 # # Epoch 15, training: loss: 0.26191 # # Epoch 15, validation: loss: 0.35338 # # Epoch 16, training: loss: 0.25533 # # Epoch 16, validation: loss: 0.35453 # # Epoch 17, training: loss: 0.25085 # # Epoch 17, validation: loss: 0.34521 # # Epoch 18, training: loss: 0.24686 # # Epoch 18, validation: loss: 0.35094 # # Epoch 19, training: loss: 0.24159 # # Epoch 19, validation: loss: 0.33776 # # Epoch 20, training: loss: 0.23680 # # Epoch 20, validation: loss: 0.33974 # # Epoch 21, training: loss: 0.23070 # # Epoch 21, validation: loss: 0.34069 # # Epoch 22, training: loss: 0.22761 # # Epoch 22, validation: loss: 0.33724 # # Epoch 23, training: loss: 0.22390 # # Epoch 23, validation: loss: 0.34013 # # Epoch 24, training: loss: 0.22155 # # Epoch 24, validation: loss: 0.33460 # # Epoch 25, training: loss: 0.21820 # # Epoch 25, validation: loss: 0.33755 # # Epoch 26, training: loss: 0.22134 # # Epoch 26, validation: loss: 0.33678 # # Epoch 27, training: loss: 0.21061 # # Epoch 27, validation: loss: 0.33108 # # Epoch 28, training: loss: 0.20496 # # Epoch 28, validation: loss: 0.32769 # # Epoch 29, training: loss: 0.20223 # # Epoch 29, validation: loss: 0.32969 # # Epoch 30, training: loss: 0.20022 # # Epoch 30, validation: loss: 0.33331
From the way loss decreases on the training set, we conclude that, yes, the model is learning something. It probably would continue improving for quite some epochs still. We do, however, see less of an improvement on the validation set.
Naturally, now we’re curious about test-set predictions. (Remember, for testing we’re choosing the “particularly hard” month of January, 2014 – particularly hard because of a heatwave that resulted in exceptionally high demand.)
Evaluation
With no loop to be coded, evaluation now becomes pretty straightforward:
net$eval()
test_preds <- vector(mode = "list", length = length(test_dl))
i <- 1
coro::loop(for (b in test_dl) {
input <- b$x
output <- net(input$to(device = device))
preds <- as.numeric(output)
test_preds[[i]] <- preds
i <<- i + 1
})
vic_elec_jan_2014 <- vic_elec %>%
filter(year(Date) == 2014, month(Date) == 1)
test_pred1 <- test_preds[[1]]
test_pred1 <- c(rep(NA, n_timesteps), test_pred1, rep(NA, nrow(vic_elec_jan_2014) - n_timesteps - n_forecast))
test_pred2 <- test_preds[[408]]
test_pred2 <- c(rep(NA, n_timesteps + 407), test_pred2, rep(NA, nrow(vic_elec_jan_2014) - 407 - n_timesteps - n_forecast))
test_pred3 <- test_preds[[817]]
test_pred3 <- c(rep(NA, nrow(vic_elec_jan_2014) - n_forecast), test_pred3)
preds_ts <- vic_elec_jan_2014 %>%
select(Demand) %>%
add_column(
mlp_ex_1 = test_pred1 * train_sd + train_mean,
mlp_ex_2 = test_pred2 * train_sd + train_mean,
mlp_ex_3 = test_pred3 * train_sd + train_mean) %>%
pivot_longer(-Time) %>%
update_tsibble(key = name)
preds_ts %>%
autoplot() +
scale_colour_manual(values = c("#08c5d1", "#00353f", "#ffbf66", "#d46f4d")) +
theme_minimal()

(#fig:unnamed-chunk-6)One-week-ahead predictions for January, 2014.
Compare this to the forecast obtained by feeding back predictions. The demand profiles over the day look a lot more realistic now. How about the phases of extreme demand? Evidently, these are not reflected in the forecast, not any more than in the “loop technique”. In fact, the forecast allows for interesting insights into this model’s personality: Apparently, it really likes fluctuating around the mean – “prime” it with inputs that oscillate around a significantly higher level, and it will quickly shift back to its comfort zone.
Discussion
Seeing how, above, we provided an option to use dropout inside the MLP, you may be wondering if this would help with forecasts on the test set. Turns out it did not, in my experiments. Maybe this is not so strange either: How, absent external cues (temperature), should the network know that high demand is coming up?
In our analysis, we can make an additional distinction. With the first week of predictions, what we see is a failure to anticipate something that could not reasonably have been anticipated (two, or two-and-a-half, say, days of exceptionally high demand). In the second, all the network would have had to do was stay at the current, elevated level. It will be interesting to see how this is handled by the architectures we discuss next.
Finally, an additional idea you may have had is – what if we used temperature as a second input variable? As a matter of fact, training performance indeed improved, but no performance impact was observed on the validation and test sets. Still, you may find the code useful – it is easily extended to datasets with more predictors. Therefore, we reproduce it in the appendix.
Thanks for reading!
Appendix
# Data input code modified to accommodate two predictors
n_timesteps <- 7 * 24 * 2
n_forecast <- 7 * 24 * 2
vic_elec_get_year <- function(year, month = NULL) {
vic_elec %>%
filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else month) %>%
as_tibble() %>%
select(Demand, Temperature)
}
elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix()
train_mean_demand <- mean(elec_train[ , 1])
train_sd_demand <- sd(elec_train[ , 1])
train_mean_temp <- mean(elec_train[ , 2])
train_sd_temp <- sd(elec_train[ , 2])
elec_dataset <- dataset(
name = "elec_dataset",
initialize = function(data, n_timesteps, n_forecast, sample_frac = 1) {
demand <- (data[ , 1] - train_mean_demand) / train_sd_demand
temp <- (data[ , 2] - train_mean_temp) / train_sd_temp
self$x <- cbind(demand, temp) %>% torch_tensor()
self$n_timesteps <- n_timesteps
self$n_forecast <- n_forecast
n <- nrow(self$x) - self$n_timesteps - self$n_forecast + 1
self$starts <- sort(sample.int(
n = n,
size = n * sample_frac
))
},
.getitem = function(i) {
start <- self$starts[i]
end <- start + self$n_timesteps - 1
pred_length <- self$n_forecast
list(
x = self$x[start:end, ],
y = self$x[(end + 1):(end + pred_length), 1]
)
},
.length = function() {
length(self$starts)
}
)
### rest identical to single-predictor code above
Photo by Monica Bourgeau on Unsplash
Tutorial: Unlocking the Promise of 5G
 The focus of this post is on using commercial off-the-shelf (COTS) hardware running BIG-IP VE with NVIDIA NICs and switches to achieve 100G+ throughput in an ultra-high, high-density solution that is available today.
The focus of this post is on using commercial off-the-shelf (COTS) hardware running BIG-IP VE with NVIDIA NICs and switches to achieve 100G+ throughput in an ultra-high, high-density solution that is available today. 
The focus of this demo is on using commercial off-the-shelf (COTS) hardware running BIG-IP VE with NVIDIA NICs and switches to achieve 100G+ throughput in an ultra-high, high-density solution that is available for purchase today.
 With this latest .4 release, NVIDIA Merlin delivers a new API and inference support that helps streamline the recommender workflow.
With this latest .4 release, NVIDIA Merlin delivers a new API and inference support that helps streamline the recommender workflow.
Relevant recommenders have the potential to impact millions of human decisions each day and build trust. Today, data scientists and machine learning engineers responsible for building relevant and impactful recommenders face challenges including slow pipelines, large embedding tables exceeding memory, and maintaining high throughput while maintaining low latency. These challenges are not inconsequential and can provide obstacles to frequently training, retraining, or deploying models into production. With this latest .4 release, NVIDIA Merlin delivers a new API and inference support that helps streamline the recommender workflow.
Why Deep Learning for Recommenders?
Deep learning techniques enable machine learning engineers and data scientists to build fresh and relevant recommenders on large datasets at scale. Merlin [https://developer.nvidia.com/nvidia-merlin] democratizes building effective deep learning recommenders with open source components including: NVTabular, a preprocessing and feature engineering library; HugeCTR, a training framework created to handle large embedding tables; and Triton Inference Server which enables model deployment.
Merlin Inference
With Merlin .4, both NVTabular and HugeCTR deepen inference support and integration with Triton Inference Server. As Triton Inference Server provides high performance throughput with low latency when deploying models, Merlin’s reinforces NVIDIA’s commitment to tackling common recommender challenges and accelerating workflows.
Merlin API: Ease of Use
Merlin currently in open beta and NVIDIA reaffirms commitment to streamlining recommender workflows by incorporating customer feedback into each release. The latest high level Merlin API makes it easier to define workflows and training pipelines.

Download and Try All of Merlin Components
Building fresh and relevant recommenders at scale is a known challenge. Data scientists and machine learning engineers tackle these recommender challenges with a variety, or hybrid, of tools, techniques, and algorithms. Merlin is interoperable, designed to support machine learning engineers and scientists with preprocessing, feature engineering, training, and inference that helps provide relevant, impactful, and fresh recommenders at scale. If interested in accelerating recommender workflows and trying out an end-to-end deep learning recommender framework, visit the Merlin product home page or download from the NGC catalog.
 Through the tutorial, you will create a QA service with Bidirectional Encoder Representations from Transformers (BERT).
Through the tutorial, you will create a QA service with Bidirectional Encoder Representations from Transformers (BERT).
Through the tutorial, you will create a QA service with Bidirectional Encoder Representations from Transformers (BERT).
 Telcos require fast, time-synchronized, precise, affordable, and secure networking for 5G rollouts. The key to this is a solution that offers high programmability, scalability, and performance combined with intelligent accelerators and offloads with low-latency and fast packet processing capabilities and GPU acceleration at the edge.
Telcos require fast, time-synchronized, precise, affordable, and secure networking for 5G rollouts. The key to this is a solution that offers high programmability, scalability, and performance combined with intelligent accelerators and offloads with low-latency and fast packet processing capabilities and GPU acceleration at the edge.
Telcos require fast, time-synchronized, precise, affordable, and secure networking for 5G rollouts. The key to this is a solution that offers high programmability, scalability, and performance combined with intelligent accelerators and offloads with low-latency and fast packet processing capabilities and GPU acceleration at the edge.
