Ranking is a core problem across a variety of domains, such as search engines, recommendation systems, or question answering. As such, researchers often utilize learning-to-rank (LTR), a set of supervised machine learning techniques that optimize for the utility of an entire list of items (rather than a single item at a time). A noticeable recent focus is on combining LTR with deep learning. Existing libraries, most notably TF-Ranking, offer researchers and practitioners the necessary tools to use LTR in their work. However, none of the existing LTR libraries work natively with JAX, a new machine learning framework that provides an extensible system of function transformations that compose: automatic differentiation, JIT-compilation to GPU/TPU devices and more.
Today, we are excited to introduce Rax, a library for LTR in the JAX ecosystem. Rax brings decades of LTR research to the JAX ecosystem, making it possible to apply JAX to a variety of ranking problems and combine ranking techniques with recent advances in deep learning built upon JAX (e.g., T5X). Rax provides state-of-the-art ranking losses, a number of standard ranking metrics, and a set of function transformations to enable ranking metric optimization. All this functionality is provided with a well-documented and easy to use API that will look and feel familiar to JAX users. Please check out our paper for more technical details.
Learning-to-Rank Using Rax
Rax is designed to solve LTR problems. To this end, Rax provides loss and metric functions that operate on batches of lists, not batches of individual data points as is common in other machine learning problems. An example of such a list is the multiple potential results from a search engine query. The figure below illustrates how tools from Rax can be used to train neural networks on ranking tasks. In this example, the green items (B, F) are very relevant, the yellow items (C, E) are somewhat relevant and the red items (A, D) are not relevant. A neural network is used to predict a relevancy score for each item, then these items are sorted by these scores to produce a ranking. A Rax ranking loss incorporates the entire list of scores to optimize the neural network, improving the overall ranking of the items. After several iterations of stochastic gradient descent, the neural network learns to score the items such that the resulting ranking is optimal: relevant items are placed at the top of the list and non-relevant items at the bottom.
 |
| Using Rax to optimize a neural network for a ranking task. The green items (B, F) are very relevant, the yellow items (C, E) are somewhat relevant and the red items (A, D) are not relevant. |
Approximate Metric Optimization
The quality of a ranking is commonly evaluated using ranking metrics, e.g., the normalized discounted cumulative gain (NDCG). An important objective of LTR is to optimize a neural network so that it scores highly on ranking metrics. However, ranking metrics like NDCG can present challenges because they are often discontinuous and flat, so stochastic gradient descent cannot directly be applied to these metrics. Rax provides state-of-the-art approximation techniques that make it possible to produce differentiable surrogates to ranking metrics that permit optimization via gradient descent. The figure below illustrates the use of rax.approx_t12n, a function transformation unique to Rax, which allows for the NDCG metric to be transformed into an approximate and differentiable form.
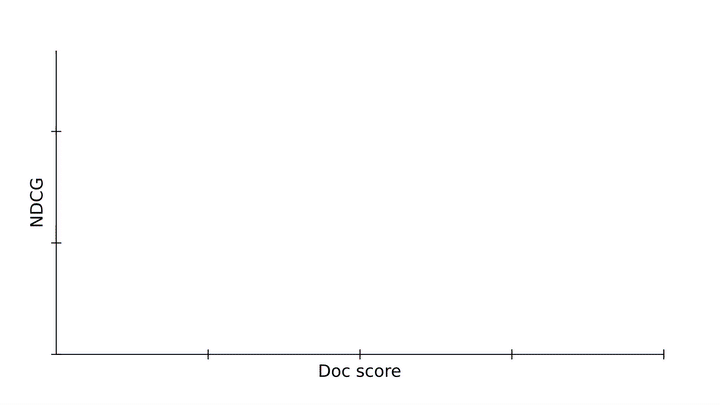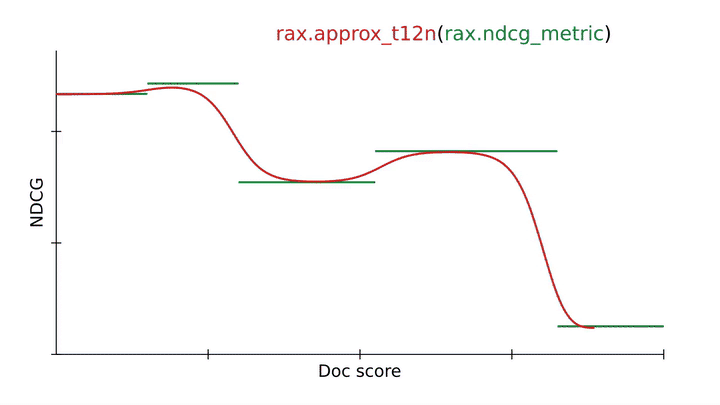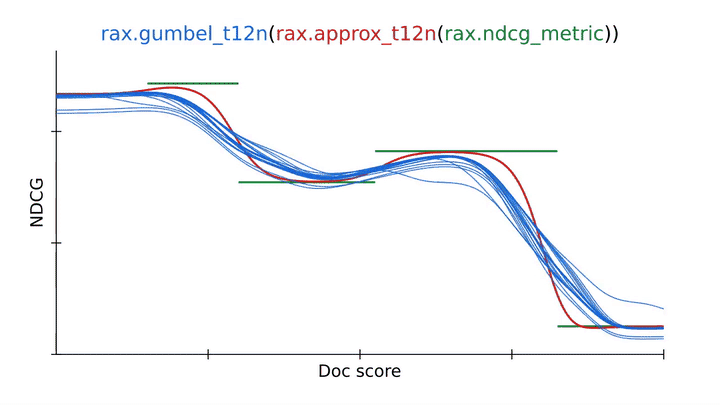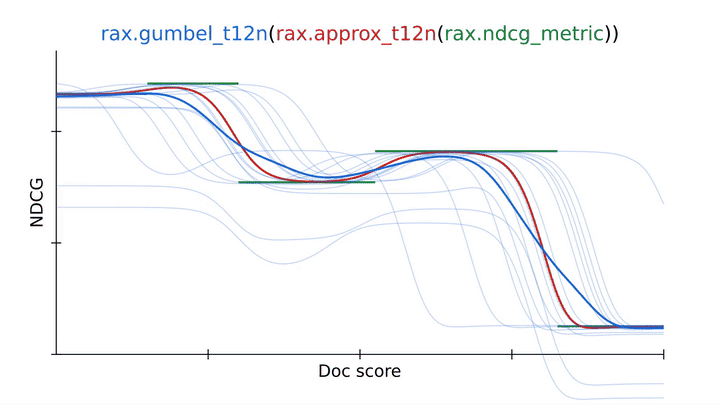 |
Using an approximation technique from Rax to transform the NDCG ranking metric into a differentiable and optimizable ranking loss (approx_t12n and gumbel_t12n). |
First, notice how the NDCG metric (in green) is flat and discontinuous, making it hard to optimize using stochastic gradient descent. By applying the rax.approx_t12n transformation to the metric, we obtain ApproxNDCG, an approximate metric that is now differentiable with well-defined gradients (in red). However, it potentially has many local optima — points where the loss is locally optimal, but not globally optimal — in which the training process can get stuck. When the loss encounters such a local optimum, training procedures like stochastic gradient descent will have difficulty improving the neural network further.
To overcome this, we can obtain the gumbel-version of ApproxNDCG by using the rax.gumbel_t12n transformation. This gumbel version introduces noise in the ranking scores which causes the loss to sample many different rankings that may incur a non-zero cost (in blue). This stochastic treatment may help the loss escape local optima and often is a better choice when training a neural network on a ranking metric. Rax, by design, allows the approximate and gumbel transformations to be freely used with all metrics that are offered by the library, including metrics with a top-k cutoff value, like recall or precision. In fact, it is even possible to implement your own metrics and transform them to obtain gumbel-approximate versions that permit optimization without any extra effort.
Ranking in the JAX Ecosystem
Rax is designed to integrate well in the JAX ecosystem and we prioritize interoperability with other JAX-based libraries. For example, a common workflow for researchers that use JAX is to use TensorFlow Datasets to load a dataset, Flax to build a neural network, and Optax to optimize the parameters of the network. Each of these libraries composes well with the others and the composition of these tools is what makes working with JAX both flexible and powerful. For researchers and practitioners of ranking systems, the JAX ecosystem was previously missing LTR functionality, and Rax fills this gap by providing a collection of ranking losses and metrics. We have carefully constructed Rax to function natively with standard JAX transformations such as jax.jit and jax.grad and various libraries like Flax and Optax. This means that users can freely use their favorite JAX and Rax tools together.
Ranking with T5
While giant language models such as T5 have shown great performance on natural language tasks, how to leverage ranking losses to improve their performance on ranking tasks, such as search or question answering, is under-explored. With Rax, it is possible to fully tap this potential. Rax is written as a JAX-first library, thus it is easy to integrate it with other JAX libraries. Since T5X is an implementation of T5 in the JAX ecosystem, Rax can work with it seamlessly.
To this end, we have an example that demonstrates how Rax can be used in T5X. By incorporating ranking losses and metrics, it is now possible to fine-tune T5 for ranking problems, and our results indicate that enhancing T5 with ranking losses can offer significant performance improvements. For example, on the MS-MARCO QNA v2.1 benchmark we are able to achieve a +1.2% NDCG and +1.7% MRR by fine-tuning a T5-Base model using the Rax listwise softmax cross-entropy loss instead of a pointwise sigmoid cross-entropy loss.
 |
| Fine-tuning a T5-Base model on MS-MARCO QNA v2.1 with a ranking loss (softmax, in blue) versus a non-ranking loss (pointwise sigmoid, in red). |
Conclusion
Overall, Rax is a new addition to the growing ecosystem of JAX libraries. Rax is entirely open source and available to everyone at github.com/google/rax. More technical details can also be found in our paper. We encourage everyone to explore the examples included in the github repository: (1) optimizing a neural network with Flax and Optax, (2) comparing different approximate metric optimization techniques, and (3) how to integrate Rax with T5X.
Acknowledgements
Many collaborators within Google made this project possible: Xuanhui Wang, Zhen Qin, Le Yan, Rama Kumar Pasumarthi, Michael Bendersky, Marc Najork, Fernando Diaz, Ryan Doherty, Afroz Mohiuddin, and Samer Hassan.
