Posted by Jaqui Herman and Cat Armato, Program Managers
This week marks the beginning of the 34th annual Conference on Neural Information Processing Systems (NeurIPS 2020), the biggest machine learning conference of the year. Held virtually for the first time, this conference includes invited talks, demonstrations and presentations of some of the latest in machine learning research. As a Platinum Sponsor of NeurIPS 2020, Google will have a strong presence with more than 180 accepted papers, additionally contributing to and learning from the broader academic research community via talks, posters, workshops and tutorials.
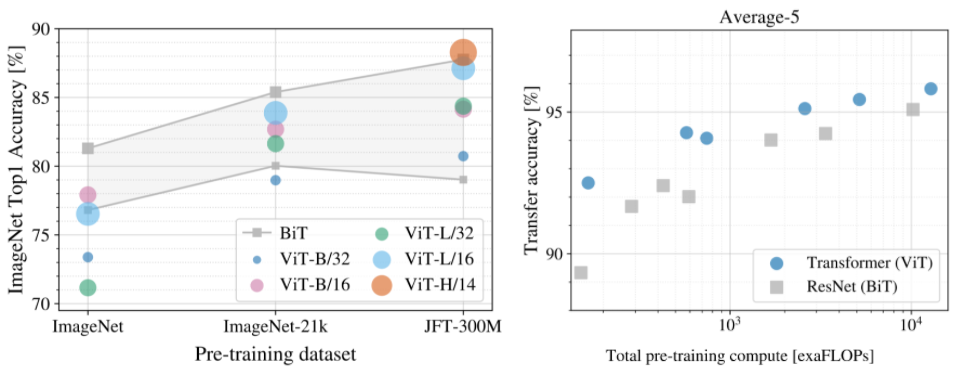
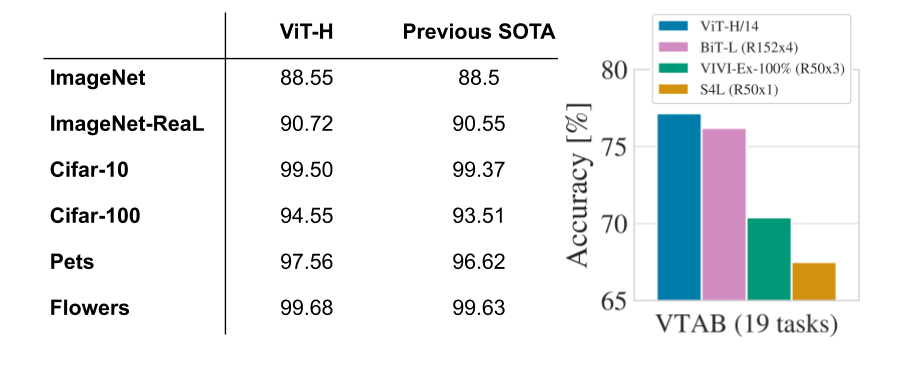
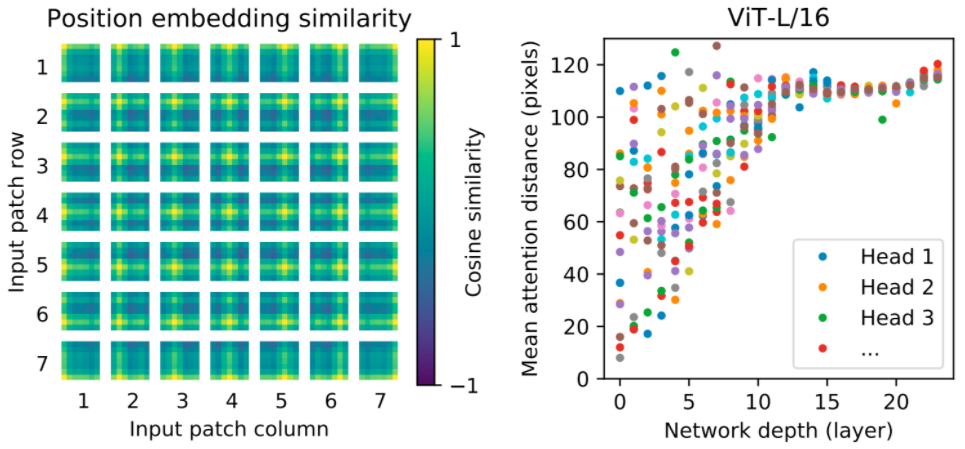
If you are registered for NeurIPS 2020, we hope you’ll visit our virtual booth and chat with our researchers about the projects and opportunities at Google that go into solving the world’s most challenging research problems, and to see demonstrations of some of the exciting research we pursue, such as Transformers for image recognition, Tone Transfer, large-scale distributed RL, recreating historical streetscapes and much more. You can also learn more about our work being presented in the list below (Google affiliations highlighted in blue).
Organizing Committees
General Chair: Hugo Larochelle
Workshop Co-Chair: Sanmi Koyejo
Diversity and Inclusion Chairs include: Katherine Heller
Expo Chair: Pablo Samuel Castro
Senior Area Chairs include: Corinna Cortes, Fei Sha, Mohammad Ghavamzadeh, Sanjiv Kumar, Charles Sutton, Dale Schuurmans, David Duvenaud, Elad Hazan, Marco Cuturi, Peter Bartlett, Samy Bengio, Tong Zhang, Claudio Gentile, Kevin Murphy, Cordelia Schmid, Amir Globerson
Area Chairs include: Boqing Gong, Afshin Rostamizadeh, Alex Kulesza, Branislav Kveton, Craig Boutilier, Heinrich Jiang, Manzil Zaheer, Silvio Lattanzi, Slav Petrov, Srinadh Bhojanapalli, Rodolphe Jenatton, Mathieu Blondel, Aleksandra Faust, Alexey Dosovitskiy, Ashish Vaswani, Augustus Odena, Balaji Lakshminarayanan, Ben Poole, Colin Raffel, Danny Tarlow, David Ha, Denny Zhou, Dumitru Erhan, Dustin Tran, George Tucker, Honglak Lee, Ilya Tolstikhin, Jasper Snoek, Jean-Philippe Vert, Jeffrey Pennington, Kevin Swersky, Matthew Johnson, Minmin Chen, Mohammad Norouzi, Moustapha Cisse, Naman Agarwal, Nicholas Carlini, Olivier Bachem, Tim Salimans, Vincent Dumoulin, Yann Dauphin, Andrew Dai, Izhak Shafran, Karthik Sridharan, Abhinav Gupta, Abhishek Kumar, Adam White, Aditya Menon, Kun Zhang, Ce Liu, Cristian Sminchisescu, Hossein Mobahi, Phillip Isola, Tomer Koren, Chelsea Finn, Amin Karbasi
NeurIPS 2020 Foundation Board includes: Michael Mozer, Samy Bengio, Corinna Cortes, Hugo Larochelle, John C. Platt, Fernando Pereira
Accepted Papers
Rankmax: An Adaptive Projection Alternative to the Softmax Function
Weiwei Kong*, Walid Krichene, Nicolas Mayoraz, Steffen Rendle, Li Zhang
Unsupervised Sound Separation Using Mixture Invariant Training
Scott Wisdom, Efthymios Tzinis*, Hakan Erdogan, Ron Weiss, Kevin Wilson, John Hershey
Learning to Select Best Forecast Tasks for Clinical Outcome Prediction
Yuan Xue, Nan Du, Anne Mottram, Martin Seneviratne, Andrew M. Dai
Interpretable Sequence Learning for Covid-19 Forecasting
Sercan O. Arık, Chun-Liang Li, Jinsung Yoon, Rajarishi Sinha, Arkady Epshteyn, Long T. Le, Vikas Menon, Shashank Singh, Leyou Zhang, Nate Yoder, Martin Nikoltchev, Yash Sonthalia, Hootan Nakhost, Elli Kanal, Tomas Pfister
Towards Learning Convolutions from Scratch
Behnam Neyshabur
Emergent Complexity and Zero-shot Transfer via Unsupervised Environment Design
Michael Dennis, Natasha Jaques, Eugene Vinitsky, Alexandre Bayen, Stuart Russell, Andrew Critch, Sergey Levine
Inverse Rational Control with Partially Observable Continuous Nonlinear Dynamics
Minhae Kwon, Saurabh Daptardar, Paul Schrater, Xaq Pitkow
Off-Policy Evaluation via the Regularized Lagrangian
Mengjiao Yang, Ofir Nachum, Bo Dai, Lihong Li, Dale Schuurmans
CoinDICE: Off-Policy Confidence Interval Estimation
Bo Dai, Ofir Nachum, Yinlam Chow, Lihong Li, Csaba Szepesvári, Dale Schuurmans
Unsupervised Data Augmentation for Consistency Training
Qizhe Xie, Zihang Dai, Eduard Hovy, Minh-Thang Luong, Quoc V. Le
VIME: Extending the Success of Self- and Semi-supervised Learning to Tabular Domain
Jinsung Yoon, Yao Zhang, James Jordon, Mihaela van der Schaar
Funnel-Transformer: Filtering out Sequential Redundancy for Efficient Language Processing
Zihang Dai, Guokun Lai, Yiming Yang, Quoc Le
Big Bird: Transformers for Longer Sequences
Manzil Zaheer, Guru Guruganesh, Avinava Dubey, Joshua Ainslie, Chris Alberti, Santiago Ontanon, Philip Pham, Anirudh Ravula, Qifan Wang, Li Yang, Amr Ahmed
Provably Efficient Neural Estimation of Structural Equation Models: An Adversarial Approach
Luofeng Liao, You-Lin Chen, Zhuoran Yang, Bo Dai, Zhaoran Wang, Mladen Kolar
Conservative Q-Learning for Offline Reinforcement Learning
Aviral Kumar, Aurick Zhou, George Tucker, Sergey Levine
MOReL: Model-Based Offline Reinforcement Learning
Rahul Kidambi, Aravind Rajeswaran, Praneeth Netrapalli, Thorsten Joachims
Maximum-Entropy Adversarial Data Augmentation for Improved Generalization and Robustness
Long Zhao, Ting Liu, Xi Peng, Dimitris Metaxas
Generative View Synthesis: From Single-view Semantics to Novel-view Images
Tewodros Habtegebrial, Varun Jampani, Orazio Gallo, Didier Stricker
PIE-NET: Parametric Inference of Point Cloud Edges
Xiaogang Wang, Yuelang Xu, Kai Xu, Andrea Tagliasacchi, Bin Zhou, Ali Mahdavi-Amiri, Hao Zhang
Enabling Certification of Verification-Agnostic Networks via Memory-Efficient Semidefinite Programming
Sumanth Dathathri, Krishnamurthy (Dj) Dvijotham, Alex Kurakin, Aditi Raghunathan, Jonathan Uesato, Rudy Bunel, Shreya Shankar, Jacob Steinhardt, Ian Goodfellow*, Percy Liang, Pushmeet Kohli
An Analysis of SVD for Deep Rotation Estimation
Jake Levinson, Carlos Esteves, Kefan Chen, Noah Snavely, Angjoo Kanazawa, Afshin Rostamizadeh, Ameesh Makadia
Direct Policy Gradients: Direct Optimization of Policies in Discrete Action Spaces
Guy Lorberbom, Chris J. Maddison, Nicolas Heess, Tamir Hazan, Daniel Tarlow
Faster Differentially Private Samplers via Rényi Divergence Analysis of Discretized Langevin MCMC
Arun Ganesh*, Kunal Talwar*
DISK: Learning Local Features with Policy Gradient
Michał J. Tyszkiewicz, Pascal Fua, Eduard Trulls
Robust Large-margin Learning in Hyperbolic Space
Melanie Weber*, Manzil Zaheer, Ankit Singh Rawat, Aditya Menon, Sanjiv Kumar
Gamma-Models: Generative Temporal Difference Learning for Infinite-Horizon Prediction
Michael Janner, Igor Mordatch, Sergey Levine
Adversarially Robust Streaming Algorithms via Differential Privacy
Avinatan Hassidim, Haim Kaplan, Yishay Mansour, Yossi Matias, Uri Stemmer
Faster DBSCAN via Subsampled Similarity Queries
Heinrich Jiang, Jennifer Jang, Jakub Łacki
Exact Recovery of Mangled Clusters with Same-Cluster Queries
Marco Bressan, Nicolò Cesa-Bianchi, Silvio Lattanzi, Andrea Paudice
A Maximum-Entropy Approach to Off-Policy Evaluation in Average-Reward MDPs
Nevena Lazic, Dong Yin, Mehrdad Farajtabar, Nir Levine, Dilan Görür, Chris Harris, Dale Schuurmans
Fairness in Streaming Submodular Maximization: Algorithms and Hardness
Marwa El Halabi, Slobodan Mitrović, Ashkan Norouzi-Fard, Jakab Tardos, Jakub Tarnawski
Efficient Active Learning of Sparse Halfspaces with Arbitrary Bounded Noise
Chicheng Zhang, Jie Shen, Pranjal Awasthi
Private Learning of Halfspaces: Simplifying the Construction and Reducing the Sample Complexity
Haim Kaplan, Yishay Mansour, Uri Stemmer, Eliad Tsfadia
Synthetic Data Generators — Sequential and Private
Olivier Bousquet, Roi Livni, Shay Moran
Learning Discrete Distributions: User vs Item-level Privacy
Yuhan Liu, Ananda Theertha Suresh, Felix Xinnan X. Yu, Sanjiv Kumar, Michael Riley
Learning Differential Equations that are Easy to Solve
Jacob Kelly, Jesse Bettencourt, Matthew J. Johnson, David K. Duvenaud
An Optimal Elimination Algorithm for Learning a Best Arm
Avinatan Hassidim, Ron Kupfer, Yaron Singer
The Convex Relaxation Barrier, Revisited: Tightened Single-Neuron Relaxations for Neural Network Verification
Christian Tjandraatmadja, Ross Anderson, Joey Huchette, Will Ma, Krunal Kishor Patel*, Juan Pablo Vielma
Escaping the Gravitational Pull of Softmax
Jincheng Mei, Chenjun Xiao, Bo Dai, Lihong Li*, Csaba Szepesvari, Dale Schuurmans
The Complexity of Adversarially Robust Proper Learning of Halfspaces with Agnostic Noise
Ilias Diakonikolas, Daniel M. Kane, Pasin Manurangsi
PAC-Bayes Learning Bounds for Sample-Dependent Priors
Pranjal Awasthi, Satyen Kale, Stefani Karp, Mehryar Mohri
Fictitious Play for Mean Field Games: Continuous Time Analysis and Applications
Sarah Perrin, Julien Perolat, Mathieu Lauriere, Matthieu Geist, Romuald Elie, Olivier Pietquin
What Do Neural Networks Learn When Trained With Random Labels?
Hartmut Maennel, Ibrahim M. Alabdulmohsin, Ilya O. Tolstikhin, Robert Baldock*, Olivier Bousquet, Sylvain Gelly, Daniel Keysers
Online Planning with Lookahead Policies
Yonathan Efroni, Mohammad Ghavamzadeh, Shie Mannor
Smoothly Bounding User Contributions in Differential Privacy
Alessandro Epasto, Mohammad Mahdian, Jieming Mao, Vahab Mirrokni, Lijie Ren
Differentially Private Clustering: Tight Approximation Ratios
Badih Ghazi, Ravi Kumar, Pasin Manurangsi
Hitting the High Notes: Subset Selection for Maximizing Expected Order Statistics
Aranyak Mehta, Uri Nadav, Alexandros Psomas*, Aviad Rubinstein
Myersonian Regression
Allen Liu, Renato Leme, Jon Schneider
Assisted Learning: A Framework for Multi-Organization Learning
Xun Xian, Xinran Wang, Jie Ding, Reza Ghanadan
Adversarial Robustness via Robust Low Rank Representations
Pranjal Awasthi, Himanshu Jain, Ankit Singh Rawat, Aravindan Vijayaraghavan
Multi-Plane Program Induction with 3D Box Priors
Yikai Li, Jiayuan Mao, Xiuming Zhang, Bill Freeman, Josh Tenenbaum, Noah Snavely, Jiajun Wu
Privacy Amplification via Random Check-Ins
Borja Balle, Peter Kairouz, Brendan McMahan, Om Dipakbhai Thakkar, Abhradeep Thakurta
Rethinking Pre-training and Self-training
Barret Zoph, Golnaz Ghiasi, Tsung-Yi Lin, Yin Cui, Hanxiao Liu, Ekin Dogus Cubuk, Quoc Le
Reinforcement Learning with Combinatorial Actions: An Application to Vehicle Routing
Arthur Delarue, Ross Anderson, Christian Tjandraatmadja
Online Agnostic Boosting via Regret Minimization
Nataly Brukhim, Xinyi Chen, Elad Hazan, Shay Moran*
From Trees to Continuous Embeddings and Back: Hyperbolic Hierarchical Clustering
Ines Chami, Albert Gu, Vaggos Chatziafratis, Christopher Ré
Faithful Embeddings for Knowledge Base Queries
Haitian Sun, Andrew Arnold*, Tania Bedrax Weiss, Fernando Pereira, William W. Cohen
Contextual Reserve Price Optimization in Auctions via Mixed Integer Programming
Joey Huchette, Haihao Lu, Hossein Esfandiari, Vahab Mirrokni
An Operator View of Policy Gradient Methods
Dibya Ghosh, Marlos C. Machado, Nicolas Le Roux
Reinforcement Learning with Feedback Graphs
Christoph Dann, Yishay Mansour, Mehryar Mohri, Ayush Sekhari, Karthik Sridharan
On Completeness-aware Concept-Based Explanations in Deep Neural Networks
Chih-Kuan Yeh, Been Kim, Sercan Arik, Chun-Liang Li, Tomas Pfister, Pradeep Ravikumar
Rewriting History with Inverse RL: Hindsight Inference for Policy Improvement
Benjamin Eysenbach, Xinyang Geng, Sergey Levine, Ruslan Salakhutdinov
The Flajolet-Martin Sketch Itself Preserves Differential Privacy: Private Counting with Minimal Space
Adam Smith, Shuang Song, Abhradeep Thakurta
What is Being Transferred in Transfer Learning?
Behnam Neyshabur, Hanie Sedghi, Chiyuan Zhang
Latent Bandits Revisited
Joey Hong, Branislav Kveton, Manzil Zaheer, Yinlam Chow, Amr Ahmed, Craig Boutilier
MetaSDF: Meta-Learning Signed Distance Functions
Vincent Sitzmann, Eric Chan, Richard Tucker, Noah Snavely, Gordon Wetzstein
Measuring Robustness to Natural Distribution Shifts in Image Classification
Rohan Taori, Achal Dave, Vaishaal Shankar, Nicholas Carlini, Benjamin Recht, Ludwig Schmidt
Robust Optimization for Fairness with Noisy Protected Groups
Serena Wang, Wenshuo Guo, Harikrishna Narasimhan, Andrew Cotter, Maya Gupta, Michael I. Jordan
Learning Discrete Energy-based Models via Auxiliary-variable Local Exploration
Hanjun Dai, Rishabh Singh, Bo Dai, Charles Sutton, Dale Schuurmans
Breaking the Communication-Privacy-Accuracy Trilemma
Wei-Ning Chen, Peter Kairouz, Ayfer Ozgur
Differentiable Meta-Learning of Bandit Policies
Craig Boutilier, Chih-wei Hsu, Branislav Kveton, Martin Mladenov, Csaba Szepesvari, Manzil Zaheer
Multi-Stage Influence Function
Hongge Chen*, Si Si, Yang Li, Ciprian Chelba, Sanjiv Kumar, Duane Boning, Cho-Jui Hsieh
Compositional Visual Generation with Energy Based Models
Yilun Du, Shuang Li, Igor Mordatch
O(n) Connections are Expressive Enough: Universal Approximability of Sparse Transformers
Chulhee Yun, Yin-Wen Chang, Srinadh Bhojanapalli, Ankit Singh Rawat, Sashank Reddi, Sanjiv Kumar
Curriculum By Smoothing
Samarth Sinha, Animesh Garg, Hugo Larochelle
Online Linear Optimization with Many Hints
Aditya Bhaskara, Ashok Cutkosky, Ravi Kumar, Manish Purohit
Prediction with Corrupted Expert Advice
Idan Amir, Idan Attias, Tomer Koren, Roi Livni, Yishay Mansour
Agnostic Learning with Multiple Objectives
Corinna Cortes, Mehryar Mohri, Javier Gonzalvo, Dmitry Storcheus
CoSE: Compositional Stroke Embeddings
Emre Aksan, Thomas Deselaers*, Andrea Tagliasacchi, Otmar Hilliges
Reparameterizing Mirror Descent as Gradient Descent
Ehsan Amid, Manfred K. Warmuth
Understanding Double Descent Requires A Fine-Grained Bias-Variance Decomposition
Ben Adlam, Jeffrey Pennington
DisARM: An Antithetic Gradient Estimator for Binary Latent Variables
Zhe Dong, Andriy Mnih, George Tucker
Big Self-Supervised Models are Strong Semi-Supervised Learners
Ting Chen, Simon Kornblith, Kevin Swersky, Mohammad Norouzi, Geoffrey Hinton
JAX MD: A Framework for Differentiable Physics
Samuel S. Schoenholz, Ekin D. Cubuk
Gradient Surgery for Multi-Task Learning
Tianhe Yu, Saurabh Kumar, Abhishek Gupta, Sergey Levine, Karol Hausman, Chelsea Finn
LoopReg: Self-supervised Learning of Implicit Surface Correspondences, Pose and Shape for 3D Human Mesh Registration
Bharat Lal Bhatnagar, Cristian Sminchisescu, Christian Theobalt, Gerard Pons-Moll
ICE-BeeM: Identifiable Conditional Energy-Based Deep Models Based on Nonlinear ICA
Ilyes Khemakhem, Ricardo P. Monti, Diederik P. Kingma, Aapo Hyvärinen
Demystifying Orthogonal Monte Carlo and Beyond
Han Lin, Haoxian Chen, Tianyi Zhang, Clement Laroche, Krzysztof Choromanski
FixMatch: Simplifying Semi-Supervised Learning with Consistency and Confidence
Kihyuk Sohn, David Berthelot, Chun-Liang Li, Zizhao Zhang, Nicholas Carlini, Ekin D. Cubuk, Alex Kurakin, Han Zhang, Colin Raffel
Compositional Generalization via Neural-Symbolic Stack Machines
Xinyun Chen, Chen Liang, Adams Wei Yu, Dawn Song, Denny Zhou
Universally Quantized Neural Compression
Eirikur Agustsson, Lucas Theis
Self-Distillation Amplifies Regularization in Hilbert Space
Hossein Mobahi, Mehrdad Farajtabar, Peter L. Bartlett
ShapeFlow: Learnable Deformation Flows Among 3D Shapes
Chiyu “Max” Jiang, Jingwei Huang, Andrea Tagliasacchi, Leonidas Guibas
Entropic Optimal Transport between Unbalanced Gaussian Measures has a Closed Form
Hicham Janati, Boris Muzellec, Gabriel Peyré, Marco Cuturi
High-Fidelity Generative Image Compression
Fabian Mentzer*, George Toderici, Michael Tschannen*, Eirikur Agustsson
COT-GAN: Generating Sequential Data via Causal Optimal Transport
Tianlin Xu, Li K. Wenliang, Michael Munn, Beatrice Acciaio
When Do Neural Networks Outperform Kernel Methods?
Behrooz Ghorbani, Song Mei, Theodor Misiakiewicz, Andrea Montanari
Sense and Sensitivity Analysis: Simple Post-Hoc Analysis of Bias Due to Unobserved Confounding
Victor Veitch, Anisha Zaveri
Exemplar VAE: Linking Generative Models, Nearest Neighbor Retrieval, and Data Augmentation
Sajad Norouzi, David J. Fleet, Mohamamd Norouzi
Mitigating Forgetting in Online Continual Learning via Instance-Aware Parameterization
Hung-Jen Chen, An-Chieh Cheng, Da-Cheng Juan, Wei Wei, Min Sun
Consistent Plug-in Classifiers for Complex Objectives and Constraints
Shiv Kumar Tavker, Harish Guruprasad Ramaswamy, Harikrishna Narasimhan
Online MAP Inference of Determinantal Point Processes
Aditya Bhaskara, Amin Karbasi, Silvio Lattanzi, Morteza Zadimoghaddam
Organizing Recurrent Network Dynamics by Task-computation to Enable Continual Learning
Lea Duncker, Laura Driscoll, Krishna V. Shenoy, Maneesh Sahani, David Sussillo
RL Unplugged: A Collection of Benchmarks for Offline Reinforcement Learning
Caglar Gulcehre, Ziyu Wang, Alexander Novikov, Thomas Paine, Sergio Gómez, Konrad Zolna, Rishabh Agarwal, Josh S. Merel, Daniel J. Mankowitz, Cosmin Paduraru, Gabriel Dulac-Arnold, Jerry Li, Mohammad Norouzi, Matthew Hoffman, Nicolas Heess, Nando de Freitas
Neural Execution Engines: Learning to Execute Subroutines
Yujun Yan*, Kevin Swersky, Danai Koutra, Parthasarathy Ranganathan, Milad Hashemi
Spin-Weighted Spherical CNNs
Carlos Esteves, Ameesh Makadia, Kostas Daniilidis
An Efficient Nonconvex Reformulation of Stagewise Convex Optimization Problems
Rudy R. Bunel, Oliver Hinder, Srinadh Bhojanapalli, Krishnamurthy Dvijotham
Stochastic Optimization with Laggard Data Pipelines
Naman Agarwal, Rohan Anil, Tomer Koren, Kunal Talwar*, Cyril Zhang*
Regularizing Towards Permutation Invariance In Recurrent Models
Edo Cohen-Karlik, Avichai Ben David, Amir Globerson
Fast and Accurate kk-means++ via Rejection Sampling
Vincent Cohen-Addad, Silvio Lattanzi, Ashkan Norouzi-Fard, Christian Sohler*, Ola Svensson
Fairness Without Demographics Through Adversarially Reweighted Learning
Preethi Lahoti*, Alex Beutel, Jilin Chen, Kang Lee, Flavien Prost, Nithum Thain, Xuezhi Wang, Ed Chi
Gradient Estimation with Stochastic Softmax Tricks
Max Paulus, Dami Choi, Daniel Tarlow, Andreas Krause, Chris J. Maddison
Just Pick a Sign: Optimizing Deep Multitask Models with Gradient Sign Dropout
Zhao Chen, Jiquan Ngiam, Yanping Huang, Thang Luong, Henrik Kretzschmar, Yuning Chai, Dragomir Anguelov
A Spectral Energy Distance for Parallel Speech Synthesis
Alexey A. Gritsenko, Tim Salimans, Rianne van den Berg, Jasper Snoek, Nal Kalchbrenner
Ode to an ODE
Krzysztof Choromanski, Jared Quincy Davis, Valerii Likhosherstov, Xingyou Song, Jean-Jacques Slotine, Jacob Varley, Honglak Lee, Adrian Weller, Vikas Sindhwani
RandAugment: Practical Automated Data Augmentation with a Reduced Search Space
Ekin Dogus Cubuk, Barret Zoph, Jon Shlens, Quoc Le
On Adaptive Attacks to Adversarial Example Defenses
Florian Tramer, Nicholas Carlini, Wieland Brendel, Aleksander Madry
Fair Performance Metric Elicitation
Gaurush Hiranandani, Harikrishna Narasimhan, Oluwasanmi O. Koyejo
Robust Pre-Training by Adversarial Contrastive Learning
Ziyu Jiang, Tianlong Chen, Ting Chen, Zhangyang Wang
Why are Adaptive Methods Good for Attention Models?
Jingzhao Zhang, Sai Praneeth Karimireddy, Andreas Veit, Seungyeon Kim, Sashank Reddi, Sanjiv Kumar, Suvrit Sra
PyGlove: Symbolic Programming for Automated Machine Learning
Daiyi Peng, Xuanyi Dong, Esteban Real, Mingxing Tan, Yifeng Lu, Gabriel Bender, Hanxiao Liu, Adam Kraft, Chen Liang, Quoc Le
Fair Hierarchical Clustering
Sara Ahmadian, Alessandro Epasto, Marina Knittel, Ravi Kumar, Mohammad Mahdian, Benjamin Moseley, Philip Pham, Sergei Vassilvitskii, Yuyan Wang
Fairness with Overlapping Groups; a Probabilistic Perspective
Forest Yang*, Moustapha Cisse, Sanmi Koyejo
Differentiable Top-k with Optimal Transport
Yujia Xie*, Hanjun Dai, Minshuo Chen, Bo Dai, Tuo Zhao, Hongyuan Zha, Wei Wei, Tomas Pfister
The Origins and Prevalence of Texture Bias in Convolutional Neural Networks
Katherine Hermann, Ting Chen, Simon Kornblith
Approximate Heavily-Constrained Learning with Lagrange Multiplier Models
Harikrishna Narasimhan, Andrew Cotter, Yichen Zhou, Serena Wang, Wenshuo Guo
Evaluating Attribution for Graph Neural Networks
Benjamin Sanchez-Lengeling, Jennifer Wei, Brian Lee, Emily Reif, Peter Wang, Wesley Wei Qian, Kevin McCloskey, Lucy Colwell, Alexander Wiltschko
Sliding Window Algorithms for k-Clustering Problems
Michele Borassi, Alessandro Epasto, Silvio Lattanzi, Sergei Vassilvitskii, Morteza Zadimoghaddam
Meta-Learning Requires Meta-Augmentation
Janarthanan Rajendran*, Alex Irpan, Eric Jang
What Makes for Good Views for Contrastive Learning?
Yonglong Tian, Chen Sun, Ben Poole, Dilip Krishnan, Cordelia Schmid, Phillip Isola
Supervised Contrastive Learning
Prannay Khosla*, Piotr Teterwak*, Chen Wang*, Aaron Sarna, Yonglong Tian, Phillip Isola, Aaron Maschinot, Ce Liu, Dilip Krishnan
Critic Regularized Regression
Ziyu Wang, Alexander Novikov, Konrad Zolna, Josh Merel, Jost Tobias Springenberg, Scott Reed, Bobak Shahriari, Noah Siegel, Caglar Gulcehre, Nicolas Heess, Nando de Freitas
Off-Policy Imitation Learning from Observations
Zhuangdi Zhu, Kaixiang Lin, Bo Dai, Jiayu Zhou
Effective Diversity in Population Based Reinforcement Learning
Jack Parker-Holder, Aldo Pacchiano, Krzysztof Choromanski, Stephen Roberts
Memory Based Trajectory-conditioned Policies for Learning from Sparse Rewards
Yijie Guo, Jongwook Choi, Marcin Moczulski, Shengyu Feng, Samy Bengio, Mohammad Norouzi, Honglak Lee
Object-Centric Learning with Slot Attention
Francesco Locatello*, Dirk Weissenborn, Thomas Unterthiner, Aravindh Mahendran, Georg Heigold, Jakob Uszkoreit, Alexey Dosovitskiy, Thomas Kipf
On the Power of Louvain in the Stochastic Block Model
Vincent Cohen-Addad, Adrian Kosowski, Frederik Mallmann-Trenn, David Saulpic
Learning to Execute Programs with Instruction Pointer Attention Graph Neural Networks
David Bieber, Charles Sutton, Hugo Larochelle, Daniel Tarlow
SMYRF – Efficient Attention using Asymmetric Clustering
Giannis Daras, Nikita Kitaev, Augustus Odena, Alexandros G. Dimakis
Graph Contrastive Learning with Augmentations
Yuning You, Tianlong Chen, Yongduo Sui, Ting Chen, Zhangyang Wang, Yang Shen
WOR and p’s: Sketches for ℓp-Sampling Without Replacement
Edith Cohen, Rasmus Pagh, David P. Woodruff
Fourier Features Let Networks Learn High Frequency Functions in Low Dimensional Domains
Matthew Tancik, Pratul Srinivasan, Ben Mildenhall, Sara Fridovich-Keil, Nithin Raghavan, Utkarsh Singhal, Ravi Ramamoorthi, Jonathan Barron, Ren Ng
Model Selection in Contextual Stochastic Bandit Problems
Aldo Pacchiano, My Phan, Yasin Abbasi Yadkori, Anup Rao, Julian Zimmert, Tor Lattimore, Csaba Szepesvari
Adapting to Misspecification in Contextual Bandits
Dylan J. Foster, Claudio Gentile, Mehryar Mohri, Julian Zimmert
Leverage the Average: an Analysis of KL Regularization in Reinforcement Learning
Nino Vieillard, Tadashi Kozunoú, Bruno Scherrer, Olivier Pietquin, Rémi Munos, Matthieu Geist
Learning with Differentiable Pertubed Optimizers
Quentin Berthet, Mathieu Blondel, Olivier Teboul, Marco Cuturi, Jean-Philippe Vert, Francis Bach
Munchausen Reinforcement Learning
Nino Vieillard, Olivier Pietquin, Matthieu Geist
Log-Likelihood Ratio Minimizing Flows: Towards Robust and Quantifiable Neural Distribution Alignment
Ben Usman, Avneesh Sud, Nick Dufour, Kate Saenko
Your GAN is Secretly an Energy-based Model and You Should Use Discriminator Driven Latent Sampling
Tong Che, Ruixiang Zhang, Jascha Sohl-Dickstein, Hugo Larochelle, Liam Paull, Yuan Cao, Yoshua Bengio
Sample Complexity of Uniform Convergence for Multicalibration
Eliran Shabat, Lee Cohen, Yishay Mansour
Implicit Regularization and Convergence for Weight Normalization
Xiaoxia Wu, Edgar Dobriban, Tongzheng Ren, Shanshan Wu, Zhiyuan Li, Suriya Gunasekar, Rachel Ward, Qiang Liu
Most ReLU Networks Suffer from ℓ² Adversarial Perturbations
Amit Daniely, Hadas Shacham
Geometric Exploration for Online Control
Orestis Plevrakis, Elad Hazan
PLLay: Efficient Topological Layer Based on Persistent Landscapes
Kwangho Kim, Jisu Kim, Manzil Zaheer, Joon Sik Kim, Frederic Chazal, Larry Wasserman
Simple and Principled Uncertainty Estimation with Deterministic Deep Learning via Distance Awareness
Jeremiah Zhe Liu*, Zi Lin, Shreyas Padhy, Dustin Tran, Tania Bedrax-Weiss, Balaji Lakshminarayanan
Bayesian Deep Ensembles via the Neural Tangent Kernel
Bobby He, Balaji Lakshminarayanan, Yee Whye Teh
Hyperparameter Ensembles for Robustness and Uncertainty Quantification
Florian Wenzel, Jasper Snoek, Dustin Tran, Rodolphe Jenatton
Conic Descent and its Application to Memory-efficient Optimization Over Positive Semidefinite Matrices
John Duchi, Oliver Hinder, Andrew Naber, Yinyu Ye
On the Training Dynamics of Deep Networks with L₂ Regularization
Aitor Lewkowycz, Guy Gur-Ari
The Surprising Simplicity of the Early-Time Learning Dynamics of Neural Networks
Wei Hu*, Lechao Xiao, Ben Adlam, Jeffrey Pennington
Adaptive Probing Policies for Shortest Path Routing
Aditya Bhaskara, Sreenivas Gollapudi, Kostas Kollias, Kamesh Munagala
Optimal Approximation — Smoothness Tradeoffs for Soft-Max Functions
Alessandro Epasto, Mohammad Mahdian, Vahab Mirrokni, Emmanouil Zampetakis
An Unsupervised Information-Theoretic Perceptual Quality Metric
Sangnie Bhardwaj, Ian Fischer, Johannes Ballé, Troy Chinen
Learning Graph Structure With A Finite-State Automaton Layer
Daniel Johnson, Hugo Larochelle, Daniel Tarlow
Estimating Training Data Influence by Tracing Gradient Descent
Garima Pruthi, Frederick Liu, Satyen Kale, Mukund Sundararajan
Tutorials
Designing Learning Dynamics
Organizers: Marta Garnelo, David Balduzzi, Wojciech Czarnecki
Where Neuroscience meets AI (And What’s in Store for the Future)
Organizers: Jane Wang, Kevin Miller, Adam Marblestone
Offline Reinforcement Learning: From Algorithm Design to Practical Applications
Organizers: Sergey Levine, Aviral Kumar
Practical Uncertainty Estimation and Out-of-Distribution Robustness in Deep Learning
Organizers: Dustin Tran, Balaji Lakshminarayanan, Jasper Snoek
Abstraction & Reasoning in AI systems: Modern Perspectives
Organizers: Francois Chollet, Melanie Mitchell, Christian Szegedy
Policy Optimization in Reinforcement Learning
Organizers: Sham M Kakade, Martha White, Nicolas Le Roux
Federated Learning and Analytics: Industry Meets Academia
Organizers: Brendan McMahan, Virginia Smith, Peter Kairouz
Deep Implicit Layers: Neural ODEs, Equilibrium Models, and Differentiable Optimization
Organizers: David Duvenaud, J. Zico Kolter, Matthew Johnson
Beyond Accuracy: Grounding Evaluation Metrics for Human-Machine Learning Systems
Organizers: Praveen Chandar, Fernando Diaz, Brian St. Thomas
Workshops
Black in AI Workshop @ NeurIPS 2020 (Diamond Sponsor)
Mentorship Roundtables: Natasha Jacques
LatinX in AI Workshop @ NeurIPS 2020 (Platinum Sponsor)
Organizers include: Pablo Samuel Castro
Invited Speaker: Fernanda Viégas
Mentorship Roundtables: Tomas Izo
Queer in AI Workshop @ NeurIPS 2020 (Platinum Sponsor)
Organizers include: Raphael Gontijo Lopes
Women in Machine Learning (Platinum Sponsor)
Organizers include: Xinyi Chen, Jessica Schrouff
Invited Speaker: Fernanda Viégas
Sponsor Talk: Jessica Schrouff
Mentorship Roundtables: Hanie Sedghi, Marc Bellemare, Katherine Heller, Rianne van den Berg, Natalie Schluter, Colin Raffel, Azalia Mirhoseini, Emily Denton, Jesse Engel, Anusha Ramesh, Matt Johnson, Jeff Dean, Laurent Dinh, Samy Bengio, Yasaman Bahri, Corinna Cortes, Nicolas le Roux, Hugo Larochelle, Sergio Guadarrama, Natasha Jaques, Pablo Samuel Castro, Elaine Le, Cory Silvear
Muslims in ML
Organizers include: Mohammad Norouzi
Resistance AI Workshop
Organizers include: Elliot Creager, Raphael Gontijo Lopes
Privacy Preserving Machine Learning — PriML and PPML Joint Edition
Organizers include: Adria Gascon, Mariana Raykova
OPT2020: Optimization for Machine Learning
Organizers include: Courtney Paquette
Machine Learning for Health (ML4H): Advancing Healthcare for All
Organizers include: Subhrajit Roy
Human in the Loop Dialogue Systems
Organizers include: Rahul Goel
Invited Speaker: Ankur Parikh
Self-Supervised Learning for Speech and Audio Processing
Organizers include: Tara Sainath
Invited Speaker: Bhuvana Ramabhadran
3rd Robot Learning Workshop
Organizers include: Alex Bewley, Vincent Vanhoucke
Invited Speaker: Pete Florence
Workshop on Deep Learning and Inverse Problems
Invited Speaker: Peyman Milanfar
Crowd Science Workshop: Remoteness, Fairness, and Mechanisms as Challenges of Data Supply by Humans for Automation
Invited Speakers: Lora Aroyo, Praveen Paritosh
Workshop on Fair AI in Finance
Invited Speakers: Berk Ustun, Madeleine Clare Elish
Object Representations for Learning and Reasoning
Panel Moderator: Klaus Greff
Deep Reinforcement Learning
Organizers include: Chelsea Finn
Invited Speaker: Marc Bellemare
Algorithmic Fairness Through the Lens of Causality and Interpretability
Organizers include: Awa Dieng, Jessica Schrouff, Fernando Diaz
Machine Learning for the Developing World (ML4D)
Steering Committee Member: Ernest Mwebaze
Machine Learning for Engineering Modeling, Simulation and Design
Organizers include: Stephan Hoyer
Machine Learning for Creativity and Design
Organizers include: Adam Roberts, Daphne Ippolito
Invited Speaker: Jesse Engel
Cooperative AI
Invited Speaker: Natasha Jaques
International Workshop on Scalability, Privacy, and Security in Federated Learning (SpicyFL 2020)
Invited Speaker: Brendan McMahan
Machine Learning for Molecules
Organizers include: Jennifer Wei
Invited Speaker: Benjamin Sanchez-Lengeling
Navigating the Broader Impacts of AI Research
Panelists include: Nyalleng Moorosi, Colin Raffel, Natalie Schluter, Ben Zevenbergen
Beyond BackPropagation: Novel Ideas for Training Neural Architectures
Organizers include: Yanping Huang
Differentiable Computer Vision, Graphics, and Physics in Machine Learning
Invited Speaker: Andrea Tagliasacchi
AI for Earth Sciences
Invited Speaker: Milind Tambe
Machine Learning for Mobile Health
Organizers include: Katherine Heller, Marianne Njifon
Shared Visual Representations in Human and Machine Intelligence (SVRHM)
Invited Speaker: Gamaleldin Elsayed
The Challenges of Real World Reinforcement Learning
Organizers include: Gabriel Dulac-Arnold
Invited Speaker: Chelsea Finn
Workshop on Computer Assisted Programming (CAP)
Organizers include: Charles Sutton, Augustus Odena
Self-Supervised Learning — Theory and Practice
Organizers include: Barret Zoph
Invited Speaker: Quoc V. Le
Offline Reinforcement Learning
Organizers include: Rishabh Agarwal, George Tucker
Machine Learning for Systems
Organizers include: Anna Goldie, Azalia Mirhoseini, Martin Maas
Invited Speaker: Ed Chi
Deep Learning Through Information Geometry
Organizers include: Alexander Alemi
Expo
Drifting Efficiently Through the Stratosphere Using Deep Reinforcement Learning
Organizers include: Sal Candido
Accelerating Eye Movement Research via Smartphone Gaze
Organizers include: Vidhya Navalpakkam
Mining and Learning with Graphs at Scale
Organizers include: Bryan Perozzi, Vahab Mirrokni, Jonathan Halcrow, Jakub Lacki
*Work performed while at Google