Naive Bayes (NB) is a simple but powerful probabilistic classification technique that parallelizes well and can scale to datasets of massive size. If you have been working…
Naive Bayes (NB) is a simple but powerful probabilistic classification technique that parallelizes well and can scale to datasets of massive size. If you have been working…
Naive Bayes (NB) is a simple but powerful probabilistic classification technique that parallelizes well and can scale to datasets of massive size.
If you have been working with text processing tasks in data science, you know that machine learning models can take a long time to train. Using GPU-accelerated computing on those models has often resulted in significant gains in time performance, and NB classifiers make no exception.
By using CUDA-accelerated operations, we reached a performance boost from 5–20x depending on the NB model used. A smart utilization of sparse data led to a 120x speedup for one of the models.
In this post, we present recent upgrades to the NB implementation in RAPIDS cuML and compare it to Scikit-learn’s implementation on the CPU. We provide benchmarks to demonstrate the performance benefits and walk through simple examples of each support variant of the algorithm to help you determine which is best for your use case.
What is naive Bayes?
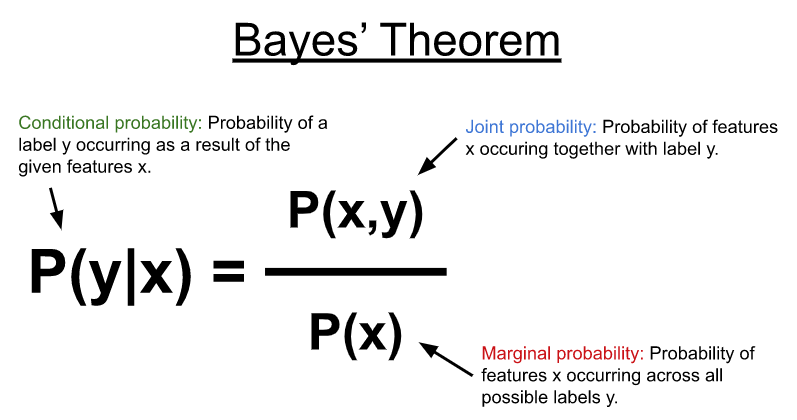
NB uses Bayes’ theorem (Figure 1) to model the conditional probability distribution shown below to predict a label or category (y) given some input features (x). In its most simplest form, the Bayes theorem computes the conditional probability using the joint probability between the features and possible labels with the marginal probability of the features occurring across all possible labels.
NB algorithms have been shown to work well on text classification use cases. They are often applied to tasks such as filtering spam emails; predicting categories and sentiment for tweets, web pages, blog posts, user ratings, and forum posts; or ranking documents and web pages.
The NB algorithms simplify the conditional probability distribution by making the naive assumption that each feature (for example, each column in an input vector x) is statistically independent of all the other features. This makes the algorithm great because this naive assumption increases the ability to parallelize the algorithm. Also, the general approach of computing simple co-occurrence probabilities between features and class labels enables the model to be trained incrementally, supporting datasets that don’t fit into memory.
NB comes in several variants, which make certain assumptions about the joint distribution or the features co-occurring with respect to various class labels.
Naive Bayes assumptions
To predict classes for unseen sets of input features, different assumptions about the joint distribution enable several different variants of the algorithm, which model the distribution of features by learning parameters for different probability distributions.
Table 1 models a simple document/term matrix that could come from a collection of text documents. The terms along the columns represent a vocabulary. A simple vocabulary might break a document into the set of unique words that occur in total across all the documents.
| I | love | dogs | hate | and | knitting | is | my | hobby | session | |
| Doc 1 | 1 | 1 | 1 | |||||||
| Doc 2 | 1 | 1 | 1 | 1 | 1 | |||||
| Doc 3 | 1 | 1 | 1 | 2 | 1 | 1 |
In Table 1, each element could be a count, such as what is shown here, a 0 or 1 to denote the existence of a feature, or some other value such as a ratio, spread, or measure of dispersion for each term occurring across the entire set of documents.
In practice, a sliding window is often run across either the entire documents or the terms, dividing them further into small chunks of word sequences, known as n-grams. For the first document of the following figure, the 2-gram (or bigram) would be “I love” and “love dogs”. It’s common for the vocabularies in these types of datasets to grow significantly large and become sparse. Preprocessing steps are often executed on the vocabulary to filter noise, for example, by removing common terms that appear in most documents.
The process of converting a document into a document-term matrix is known as vectorization. There are tools to accelerate this process, such as the CountVectorizer, TdfidfVectorizer, or HashingVectorizer estimator objects in RAPIDS cuML.
Multinomial and Bernoulli distributions
Table 1 represents a set of documents, which have been vectorized into term counts such that each element in the resulting matrix represents the number of times a particular word appears in its corresponding document. This simple representation can be effective for classification tasks.
Because the features represent a frequency distribution, the multinomial naive Bayes variant can effectively model the joint distribution of the features and their associated classes with a multinomial distribution.
The frequency distributions for each term can be enhanced by incorporating a measure of dispersion, such as Term Frequency Inverse Document Frequency (TF-IDF), which takes into account the number of documents each occurs in. This can significantly improve performance by giving more weight to the terms that appear in fewer documents, and thus improve their discriminative abilities.
While the multinomial distribution works great when used directly with term frequencies, it has also been shown to have great performance on fractional values, like TF-IDF values. The multinomial naive Bayes variant covers a great number of use cases and so tends to be the most widely used. A similar variant is Bernoulli naive Bayes, which models the simple occurrence of each term rather than their frequency, resulting in a matrix of 0s and 1s (a Bernoulli distribution).
Unequal class distributions
It’s common to find imbalanced datasets in the real world. For example, you might have limited data samples for spam and malicious activity but an abundance of normal and benign samples.
The complement naive Bayes variant helps reduce the effects of unequal class distributions by using the complement of the joint distribution for each class during training, for example, the number of times a feature occurred in samples from all other classes.
Categorical distributions
You could also create bins for each of your features, maybe by quantizing some frequencies into a number of buckets such that frequencies of 0-5 go into bucket 0, frequencies of 6-10 go into bucket 1, and so on.
Another option could be to merge several terms together into a single feature, maybe by creating buckets for “animals” and “holidays,” where “animals” might have three buckets, zero for feline, one for canine, and two for rodents. “Holidays” might have two buckets, zero for personal holidays such as a birthday or wedding anniversary, and one for federal holidays.
The categorical naive Bayes variant assumes that the features follow a categorical distribution. The naive assumption works well for this case because it allows each feature to have a different set of categories and it model the joint distribution using, you guessed it, a categorical distribution.
Continuous distributions
Finally, the Gaussian naive Bayes variant works great when features are continuous and it can be assumed that the distribution of features in each class can be modeled with Gaussian distributions, that is, with a simple mean and variance.
While this variant might demonstrate good performance on some datasets after TF-IDF normalization, it can also be useful on general machine learning datasets.
| Algorithm | Multinomial | Bernoulli | Complement | Categorical | Gaussian |
| Type of input | Frequencies, Counts |
Boolean occurrence |
Counts | Categorical | Continuous |
| Advantage | Support count data |
Support binary data |
Reduce impact of imbalance data |
Support categorical data |
Support general continuous data |
Real-world end-to-end examples
To demonstrate the benefits of each algorithm variant, as outlined in Table 2, we step through example notebooks of each algorithm variant. For a comprehensive end-to-end notebook that includes all the examples, see news_aggregator_a100.ipynb.
We used the News Aggregator dataset to demonstrate the performance of the NB variants. The dataset is available publicly from Kaggle and consists of 422K news headlines taken from multiple news sources. Each headline is labeled with one of four possible labels: business, science and technology, entertainment, and health. The data is loaded directly onto the GPU using RAPIDS cuDF and continues through preprocessing steps specific to each NB variant.
Gaussian naive Bayes
Starting with Gaussian naive Bayes, we ran a TD-IDF vectorizer to transform the text data into a real-valued vector that can be used for training.
By specifying ngram_range=(1,3) we indicated that we would learn on single words, as well as 2– and 3-grams. This increases significantly the number of terms or features to learn, from 15K words to 1.8M combinations. As most terms do not occur in most headlines, the resulting matrix is sparse with many values equal to zero. cuML supports special structures to represent data like this.
One additional benefit of NB classifiers is that they can be trained incrementally using a partial_fit method on the Estimator object. This technique is suited for massive datasets that might not fit into memory all at once or which must be distributed across multiple GPUs.
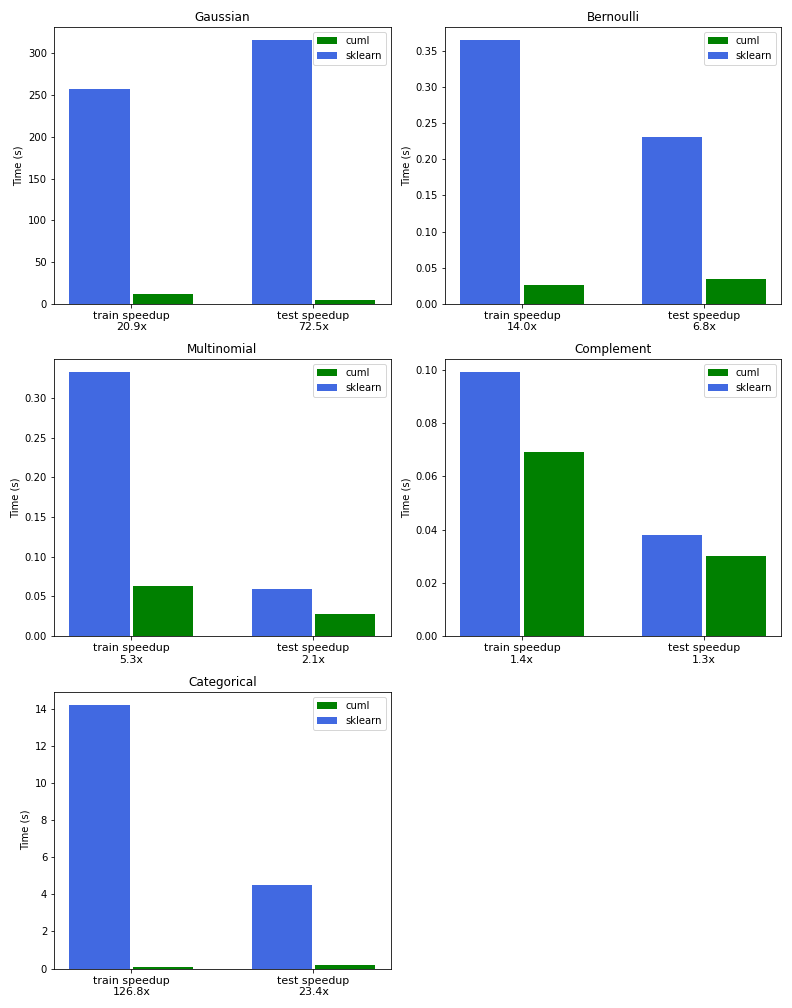
Our first example demonstrates incremental training using Gaussian naive Bayes by splitting the data into multiple chunks after preprocessing into continuous features with TF-IDF. The cuML version of Gaussian naive Bayes is 21x faster than Scikit-learn for training and 72x faster for inference.
Bernoulli naive Bayes
The next example demonstrates Bernoulli naive Bayes, without incremental training, using binary features that represent the presence or absence of each term. The CountVectorizer object can be used to accomplish this with the setting binary=True. We found a 14x speedup over Scikit-learn in this example.
Multinomial naive Bayes
Multinomial naive Bayes is the most versatile and widely used variant, as demonstrated in the following example. We used the TF-IDF vectorizer instead of CountVectorizer to achieve a 5x speedup over Scikit-learn.
Complement naive Bayes
We demonstrated the power of complement naive Bayes using CountVectorizer and showed that it yielded a better classification score than both the Bernoulli and multinomial NB variants on our imbalanced dataset.
Categorical naive Bayes
Last but definitely not least is an example of categorical naive Bayes, which we vectorized using k-means along with a model previously trained on another NB variant to group similar terms into the same categories based on their contribution to the resulting classes.
We found a 126x speedup over Scikit-learn to train a model with 315K news headlines and 23x speedup to perform inference and compute the model’s accuracy.
Benchmarks
The charts in Figure 2 compare the performance of NB training and inference between RAPIDS cuML and Scikit-learn for all of the variants outlined in this post.
The benchmarks were performed on an a2-highgpu-8g Google Cloud Platform (GCP) instance provisioned with an NVIDIA Tesla A100 GPU and 96 Intel Cascade Lake vCPUs at 2.2Ghz.
GPU-accelerated naive Bayes
We were able to implement all the NB variants right in Python with CuPy, which is a GPU-accelerated near-drop-in replacement for NumPy and SciPy. CuPy also provides you with the capability to write custom CUDA kernels in Python. It uses the just-in-time (JIT) compilation abilities of NVRTC to compile and execute them on the GPU while the Python application is running.
At the core of all the NB variants lies two simple primitives written using CuPy’s JIT, to sum and count the features for each class.
When a single document-term matrix grows too large to process on a single GPU, the Dask library can make use of the incremental training feature to spread the processing over multiple GPUs and multiple nodes. Currently, the multinomial variant can be distributed with Dask in cuML.
Conclusion
NB algorithms should be in every data scientist’s toolkit. With RAPIDS cuML you can accelerate your implementations of NB on the GPU, without dramatically changing your code. These powerful and fundamental algorithms, combined with the speedup of cuML, provide everything you must perform classification on extremely large or sparse datasets.
If you think that RAPIDS cuML can help accelerate your data science and machine learning workflows or is already doing so, then leave a comment because we’d love to hear about it.
As always, visit the rapidsai GitHub repo and let us know how we can help you. You can also follow us on Twitter at @rapidsai.
If you are new to RAPIDS, be sure to check out the Getting Started resources to get up and running quickly.