Category: Offsites

Sparklyr 1.6 is now available on CRAN!

To install sparklyr 1.6 from CRAN, run

install.packages("sparklyr")

In this blog post, we shall highlight the following features and enhancements from sparklyr 1.6:

• Weighted quantile summaries
• Power iteration clustering
• spark_write_rds() + collect_from_rds()
• Dplyr-related improvements

Weighted quantile summaries

Apache Spark is well-known for supporting approximate algorithms that trade off marginal amounts of accuracy for greater speed and parallelism. Such algorithms are particularly beneficial for performing preliminary data explorations at scale, as they enable users to quickly query certain estimated statistics within a predefined error margin, while avoiding the high cost of exact computations. One example is the Greenwald-Khanna algorithm for on-line computation of quantile summaries, as described in Greenwald and Khanna (2001). This algorithm was originally designed for efficient (epsilon)- approximation of quantiles within a large dataset without the notion of data points carrying different weights, and the unweighted version of it has been implemented as approxQuantile() since Spark 2.0. However, the same algorithm can be generalized to handle weighted inputs, and as sparklyr user @Zhuk66 mentioned in this issue, a weighted version of this algorithm makes for a useful sparklyr feature.

To properly explain what weighted-quantile means, we must clarify what the weight of each data point signifies. For example, if we have a sequence of observations ((1, 1, 1, 1, 0, 2, -1, -1)), and would like to approximate the median of all data points, then we have the following two options:

• Either run the unweighted version of approxQuantile() in Spark to scan through all 8 data points

• Or alternatively, “compress” the data into 4 tuples of (value, weight): ((1, 0.5), (0, 0.125), (2, 0.125), (-1, 0.25)), where the second component of each tuple represents how often a value occurs relative to the rest of the observed values, and then find the median by scanning through the 4 tuples using the weighted version of the Greenwald-Khanna algorithm

We can also run through a contrived example involving the standard normal distribution to illustrate the power of weighted quantile estimation in sparklyr 1.6. Suppose we cannot simply run qnorm() in R to evaluate the quantile function of the standard normal distribution at (p = 0.25) and (p = 0.75), how can we get some vague idea about the 1st and 3rd quantiles of this distribution? One way is to sample a large number of data points from this distribution, and then apply the Greenwald-Khanna algorithm to our unweighted samples, as shown below:

library(sparklyr)

sc <- spark_connect(master = "local")

num_samples <- 1e6
samples <- data.frame(x = rnorm(num_samples))

samples_sdf <- copy_to(sc, samples, name = random_string())

samples_sdf %>%
  sdf_quantile(
    column = "x",
    probabilities = c(0.25, 0.75),
    relative.error = 0.01
  ) %>%
  print()

##        25%        75%
## -0.6629242  0.6874939

Notice that because we are working with an approximate algorithm, and have specified relative.error = 0.01, the estimated value of (-0.6629242) from above could be anywhere between the 24th and the 26th percentile of all samples. In fact, it falls in the (25.36896)-th percentile:

pnorm(-0.6629242)

## [1] 0.2536896

Now how can we make use of weighted quantile estimation from sparklyr 1.6 to obtain similar results? Simple! We can sample a large number of (x) values uniformly randomly from ((-infty, infty)) (or alternatively, just select a large number of values evenly spaced between ((-M, M)) where (M) is approximately (infty)), and assign each (x) value a weight of (displaystyle frac{1}{sqrt{2 pi}}e^{-frac{x^2}{2}}), the standard normal distribution’s probability density at (x). Finally, we run the weighted version of sdf_quantile() from sparklyr 1.6, as shown below:

library(sparklyr)

sc <- spark_connect(master = "local")

num_samples <- 1e6
M <- 1000
samples <- tibble::tibble(
  x = M * seq(-num_samples / 2 + 1, num_samples / 2) / num_samples,
  weight = dnorm(x)
)

samples_sdf <- copy_to(sc, samples, name = random_string())

samples_sdf %>%
  sdf_quantile(
    column = "x",
    weight.column = "weight",
    probabilities = c(0.25, 0.75),
    relative.error = 0.01
  ) %>%
  print()

##    25%    75%
## -0.696  0.662

Voilà! The estimates are not too far off from the 25th and 75th percentiles (in relation to our abovementioned maximum permissible error of (0.01)):

pnorm(-0.696)

## [1] 0.2432144

pnorm(0.662)

## [1] 0.7460144

Power iteration clustering

Power iteration clustering (PIC), a simple and scalable graph clustering method presented in Lin and Cohen (2010), first finds a low-dimensional embedding of a dataset, using truncated power iteration on a normalized pairwise-similarity matrix of all data points, and then uses this embedding as the “cluster indicator”, an intermediate representation of the dataset that leads to fast convergence when used as input to k-means clustering. This process is very well illustrated in figure 1 of Lin and Cohen (2010) (reproduced below)

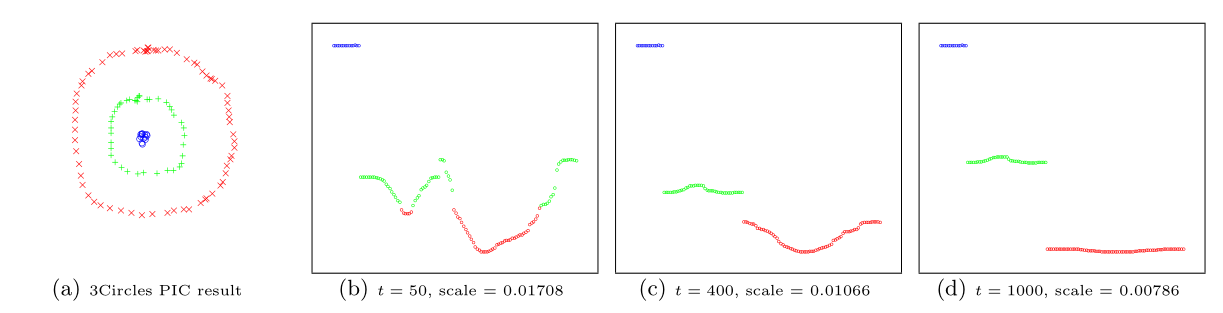
in which the leftmost image is the visualization of a dataset consisting of 3 circles, with points colored in red, green, and blue indicating clustering results, and the subsequent images show the power iteration process gradually transforming the original set of points into what appears to be three disjoint line segments, an intermediate representation that can be rapidly separated into 3 clusters using k-means clustering with (k = 3).

In sparklyr 1.6, ml_power_iteration() was implemented to make the PIC functionality in Spark accessible from R. It expects as input a 3-column Spark dataframe that represents a pairwise-similarity matrix of all data points. Two of the columns in this dataframe should contain 0-based row and column indices, and the third column should hold the corresponding similarity measure. In the example below, we will see a dataset consisting of two circles being easily separated into two clusters by ml_power_iteration(), with the Gaussian kernel being used as the similarity measure between any 2 points:

gen_similarity_matrix <- function() {
  # Guassian similarity measure
  guassian_similarity <- function(pt1, pt2) {
    exp(-sum((pt2 - pt1) ^ 2) / 2)
  }
  # generate evenly distributed points on a circle centered at the origin
  gen_circle <- function(radius, num_pts) {
    seq(0, num_pts - 1) %>%
      purrr::map_dfr(
        function(idx) {
          theta <- 2 * pi * idx / num_pts
          radius * c(x = cos(theta), y = sin(theta))
        })
  }
  # generate points on both circles
  pts <- rbind(
    gen_circle(radius = 1, num_pts = 80),
    gen_circle(radius = 4, num_pts = 80)
  )
  # populate the pairwise similarity matrix (stored as a 3-column dataframe)
  similarity_matrix <- data.frame()
  for (i in seq(2, nrow(pts)))
    similarity_matrix <- similarity_matrix %>%
      rbind(seq(i - 1L) %>%
        purrr::map_dfr(~ list(
          src = i - 1L, dst = .x - 1L,
          similarity = guassian_similarity(pts[i,], pts[.x,])
        ))
      )

  similarity_matrix
}

library(sparklyr)

sc <- spark_connect(master = "local")
sdf <- copy_to(sc, gen_similarity_matrix())
clusters <- ml_power_iteration(
  sdf, k = 2, max_iter = 10, init_mode = "degree",
  src_col = "src", dst_col = "dst", weight_col = "similarity"
)

clusters %>% print(n = 160)

## # A tibble: 160 x 2
##        id cluster
##     <dbl>   <int>
##   1     0       1
##   2     1       1
##   3     2       1
##   4     3       1
##   5     4       1
##   ...
##   157   156       0
##   158   157       0
##   159   158       0
##   160   159       0

The output shows points from the two circles being assigned to separate clusters, as expected, after only a small number of PIC iterations.

spark_write_rds() + collect_from_rds()

spark_write_rds() and collect_from_rds() are implemented as a less memory- consuming alternative to collect(). Unlike collect(), which retrieves all elements of a Spark dataframe through the Spark driver node, hence potentially causing slowness or out-of-memory failures when collecting large amounts of data, spark_write_rds(), when used in conjunction with collect_from_rds(), can retrieve all partitions of a Spark dataframe directly from Spark workers, rather than through the Spark driver node. First, spark_write_rds() will distribute the tasks of serializing Spark dataframe partitions in RDS version 2 format among Spark workers. Spark workers can then process multiple partitions in parallel, each handling one partition at a time and persisting the RDS output directly to disk, rather than sending dataframe partitions to the Spark driver node. Finally, the RDS outputs can be re-assembled to R dataframes using collect_from_rds().

Shown below is an example of spark_write_rds() + collect_from_rds() usage, where RDS outputs are first saved to HDFS, then downloaded to the local filesystem with hadoop fs -get, and finally, post-processed with collect_from_rds():

library(sparklyr)
library(nycflights13)

num_partitions <- 10L
sc <- spark_connect(master = "yarn", spark_home = "/usr/lib/spark")
flights_sdf <- copy_to(sc, flights, repartition = num_partitions)

# Spark workers serialize all partition in RDS format in parallel and write RDS
# outputs to HDFS
spark_write_rds(
  flights_sdf,
  dest_uri = "hdfs://<namenode>:8020/flights-part-{partitionId}.rds"
)

# Run `hadoop fs -get` to download RDS files from HDFS to local file system
for (partition in seq(num_partitions) - 1)
  system2(
    "hadoop",
    c("fs", "-get", sprintf("hdfs://<namenode>:8020/flights-part-%d.rds", partition))
  )

# Post-process RDS outputs
partitions <- seq(num_partitions) - 1 %>%
  lapply(function(partition) collect_from_rds(sprintf("flights-part-%d.rds", partition)))

# Optionally, call `rbind()` to combine data from all partitions into a single R dataframe
flights_df <- do.call(rbind, partitions)

Dplyr-related improvements

Similar to other recent sparklyr releases, sparklyr 1.6 comes with a number of dplyr-related improvements, such as

• Support for where() predicate within select() and summarize(across(…)) operations on Spark dataframes
• Addition of if_all() and if_any() functions
• Full compatibility with dbplyr 2.0 backend API

select(where(…)) and summarize(across(where(…)))

The dplyr where(…) construct is useful for applying a selection or aggregation function to multiple columns that satisfy some boolean predicate. For example,

library(dplyr)

iris %>% select(where(is.numeric))

returns all numeric columns from the iris dataset, and

library(dplyr)

iris %>% summarize(across(where(is.numeric), mean))

computes the average of each numeric column.

In sparklyr 1.6, both types of operations can be applied to Spark dataframes, e.g.,

library(dplyr)
library(sparklyr)

sc <- spark_connect(master = "local")
iris_sdf <- copy_to(sc, iris, name = random_string())

iris_sdf %>% select(where(is.numeric))

iris %>% summarize(across(where(is.numeric), mean))

if_all() and if_any()

if_all() and if_any() are two convenience functions from dplyr 1.0.4 (see here for more details) that effectively1 combine the results of applying a boolean predicate to a tidy selection of columns using the logical and/or operators.

Starting from sparklyr 1.6, if_all() and if_any() can also be applied to Spark dataframes, .e.g.,

library(dplyr)
library(sparklyr)

sc <- spark_connect(master = "local")
iris_sdf <- copy_to(sc, iris, name = random_string())

# Select all records with Petal.Width > 2 and Petal.Length > 2
iris_sdf %>% filter(if_all(starts_with("Petal"), ~ .x > 2))

# Select all records with Petal.Width > 5 or Petal.Length > 5
iris_sdf %>% filter(if_any(starts_with("Petal"), ~ .x > 5))

Compatibility with dbplyr 2.0 backend API

Sparklyr 1.6 is fully compatible with the newer dbplyr 2.0 backend API (by implementing all interface changes recommended in here), while still maintaining backward compatibility with the previous edition of dbplyr API, so that sparklyr users will not be forced to switch to any particular version of dbplyr.

This should be a mostly non-user-visible change as of now. In fact, the only discernible behavior change will be the following code

library(dbplyr)
library(sparklyr)

sc <- spark_connect(master = "local")

print(dbplyr_edition(sc))

outputting

[1] 2

if sparklyr is working with dbplyr 2.0+, and

[1] 1

if otherwise.

Acknowledgements

In chronological order, we would like to thank the following contributors for making sparklyr 1.6 awesome:

• @yitao-li
• @pgramme
• @javierluraschi
• @andrew-christianson
• @jozefhajnala
• @nathaneastwood
• [@mzorko] (https://github.com/mzorko)

We would also like to give a big shout-out to the wonderful open-source community behind sparklyr, without whom we would not have benefitted from numerous sparklyr-related bug reports and feature suggestions.

Finally, the author of this blog post also very much appreciates the highly valuable editorial suggestions from @skeydan.

If you wish to learn more about sparklyr, we recommend checking out sparklyr.ai, spark.rstudio.com, and also some previous sparklyr release posts such as sparklyr 1.5 and sparklyr 1.4.

That is all. Thanks for reading!

Posted by Benjamin Eysenbach, Student Researcher, Google Research

A general goal of robotics research is to design systems that can assist in a variety of tasks that can potentially improve daily life. Most reinforcement learning algorithms for teaching agents to perform new tasks require a reward function, which provides positive feedback to the agent for taking actions that lead to good outcomes. However, actually specifying these reward functions can be quite tedious and can be very difficult to define for situations without a clear objective, such as whether a room is clean or if a door is sufficiently shut. Even for tasks that are easy to describe, actually measuring whether the task has been solved can be difficult and may require adding many sensors to a robot’s environment.

Alternatively, training a model using examples, called example-based control, has the potential to overcome the limitations of approaches that rely on traditional reward functions. This new problem statement is most similar to prior methods based on “success detectors”, and efficient algorithms for example-based control could enable non-expert users to teach robots to perform new tasks, without the need for coding expertise, knowledge of reward function design, or the installation of environmental sensors.

In “Replacing Rewards with Examples: Example-Based Policy Search via Recursive Classification,” we propose a machine learning algorithm for teaching agents how to solve new tasks by providing examples of success (e.g., if “success” examples show a nail embedded into a wall, the agent will learn to pick up a hammer and knock nails into the wall). This algorithm, recursive classification of examples (RCE), does not rely on hand-crafted reward functions, distance functions, or features, but rather learns to solve tasks directly from data, requiring the agent to learn how to solve the entire task by itself, without requiring examples of any intermediate states. Using a version of temporal difference learning — similar to Q-learning, but replacing the typical reward function term using only examples of success — RCE outperforms prior approaches based on imitation learning on simulated robotics tasks. Coupled with theoretical guarantees similar to those for reward-based learning, the proposed method offers a user-friendly alternative for teaching robots new tasks.

Top: To teach a robot to hammer a nail into a wall, most reinforcement learning algorithms require that the user define a reward function. Bottom: The example-based control method uses examples of what the world looks like when a task is completed to teach the robot to solve the task, e.g., examples where the nail is already hammered into the wall.

Example-Based Control vs Imitation Learning
While the example-based control method is similar to imitation learning, there is an important distinction — it does not require expert demonstrations. In fact, the user can actually be quite bad at performing the task themselves, as long as they can look back and pick out the small fraction of states where they did happen to solve the task.

Additionally, whereas previous research used a stage-wise approach in which the model first uses success examples to learn a reward function and then applies that reward function with an off-the-shelf reinforcement learning algorithm, RCE learns directly from the examples and skips the intermediate step of defining the reward function. Doing so avoids potential bugs and bypasses the process of defining the hyperparameters associated with learning a reward function (such as how often to update the reward function or how to regularize it) and, when debugging, removes the need to examine code related to learning the reward function.

Recursive Classification of Examples
The intuition behind the RCE approach is simple: the model should predict whether the agent will solve the task in the future, given the current state of the world and the action that the agent is taking. If there were data that specified which state-action pairs lead to future success and which state-action pairs lead to future failure, then one could solve this problem using standard supervised learning. However, when the only data available consists of success examples, the system doesn’t know which states and actions led to success, and while the system also has experience interacting with the environment, this experience isn’t labeled as leading to success or not.

Left: The key idea is to learn a future success classifier that predicts for every state (circle) in a trajectory whether the task will be solved in the future (thumbs up/down). Right: In the example-based control approach, the model is provided only with unlabeled experience (grey circles) and success examples (green circles), so one cannot apply standard supervised learning. Instead, the model uses the success examples to automatically label the unlabeled experience.

Nonetheless, one can piece together what these data would look like, if it were available. First, by definition, a successful example must be one that solves the given task. Second, even though it is unknown whether an arbitrary state-action pair will lead to success in solving a task, it is possible to estimate how likely it is that the task will be solved if the agent started at the next state. If the next state is likely to lead to future success, it can be assumed that the current state is also likely to lead to future success. In effect, this is recursive classification, where the labels are inferred based on predictions at the next time step.

The underlying algorithmic idea of using a model’s predictions at a future time step as a label for the current time step closely resembles existing temporal-difference methods, such as Q-learning and successor features. The key difference is that the approach described here does not require a reward function. Nonetheless, we show that this method inherits many of the same theoretical convergence guarantees as temporal difference methods. In practice, implementing RCE requires changing only a few lines of code in an existing Q-learning implementation.

Evaluation
We evaluated the RCE method on a range of challenging robotic manipulation tasks. For example, in one task we required a robotic hand to pick up a hammer and hit a nail into a board. Previous research into this task [1, 2] have used a complex reward function (with terms corresponding to the distance between the hand and the hammer, the distance between the hammer and the nail, and whether the nail has been knocked into the board). In contrast, the RCE method requires only a few observations of what the world would look like if the nail were hammered into the board.

We compared the performance of RCE to a number of prior methods, including those that learn an explicit reward function and those based on imitation learning , all of which struggle to solve this task. This experiment highlights how example-based control makes it easy for users to specify even complex tasks, and demonstrates that recursive classification can successfully solve these sorts of tasks.

Compared with prior methods, the RCE approach solves the task of hammering a nail into a board more reliably that prior approaches based on imitation learning [SQIL, DAC] and those that learn an explicit reward function [VICE, ORIL, PURL].

Conclusion
We have presented a method to teach autonomous agents to perform tasks by providing them with examples of success, rather than meticulously designing reward functions or collecting first-person demonstrations. An important aspect of example-based control, which we discuss in the paper, is what assumptions the system makes about the capabilities of different users. Designing variants of RCE that are robust to differences in users’ capabilities may be important for applications in real-world robotics. The code is available, and the project website contains additional videos of the learned behaviors.

Acknowledgements
We thank our co-authors, Ruslan Salakhutdinov and Sergey Levine. We also thank Surya Bhupatiraju, Kamyar Ghasemipour, Max Igl, and Harini Kannan for feedback on this post, and Tom Small for helping to design figures for this post.

Posted by Aurko Roy, Research Scientist, Google Research

Open-domain long-form question answering (LFQA) is a fundamental challenge in natural language processing (NLP) that involves retrieving documents relevant to a given question and using them to generate an elaborate paragraph-length answer. While there has been remarkable recent progress in factoid open-domain question answering (QA), where a short phrase or entity is enough to answer a question, much less work has been done in the area of long-form question answering. LFQA is nevertheless an important task, especially because it provides a testbed to measure the factuality of generative text models. But, are current benchmarks and evaluation metrics really suitable for making progress on LFQA?

In “Hurdles to Progress in Long-form Question Answering” (to appear at NAACL 2021), we present a new system for open-domain long-form question answering that leverages two recent advances in NLP: 1) state-of-the-art sparse attention models, such as Routing Transformer (RT), which allow attention-based models to scale to long sequences, and 2) retrieval-based models, such as REALM, which facilitate retrievals of Wikipedia articles related to a given query. To encourage more factual grounding, our system combines information from several retrieved Wikipedia articles related to the given question before generating an answer. It achieves a new state of the art on ELI5, the only large-scale publicly available dataset for long-form question answering.

However, while our system tops the public leaderboard, we discover several troubling trends with the ELI5 dataset and its associated evaluation metrics. In particular, we find 1) little evidence that models actually use the retrievals on which they condition; 2) that trivial baselines (e.g., input copying) beat modern systems, like RAG / BART+DPR; and 3) that there is a significant train/validation overlap in the dataset. Our paper suggests mitigation strategies for each of these issues.

Text Generation
The main workhorse of NLP models is the Transformer architecture, in which each token in a sequence attends to every other token in a sequence, resulting in a model that scales quadratically with sequence length. The RT model introduces a dynamic, content-based sparse attention mechanism that reduces the complexity of attention in the Transformer model from n²to n^1.5, where n is the sequence length, which enables it to scale to long sequences. This allows each word to attend to other relevant words anywhere in the entire piece of text, unlike methods such as Transformer-XL where a word can only attend to words in its immediate vicinity.

The key insight of the RT work is that each token attending to every other token is often redundant, and may be approximated by a combination of local and global attention. Local attention allows each token to build up a local representation over several layers of the model, where each token attends to a local neighborhood, facilitating local consistency and fluency. Complementing local attention, the RT model also uses mini-batch k-means clustering to enable each token to attend only to a set of most relevant tokens.

Attention maps for the content-based sparse attention mechanism used in Routing Transformer. The word sequence is represented by the diagonal dark colored squares. In the Transformer model (left), each token attends to every other token. The shaded squares represent the tokens in the sequence to which a given token (the dark square) is attending. The RT model uses both local attention (middle), where tokens attend only to other tokens in their local neighborhood, and routing attention (right), in which a token only attends to clusters of tokens most relevant to it in context. The dark red, green and blue tokens only attend to the corresponding color of lightly shaded tokens.

We pre-train an RT model on the Project Gutenberg (PG-19) data-set with a language modeling objective, i.e, the model learns to predict the next word given all the previous words, so as to be able to generate fluent paragraph long text.

Information Retrieval
To demonstrate the effectiveness of the RT model on the task of LFQA, we combine it with retrievals from REALM. The REALM model (Guu et al. 2020) is a retrieval-based model that uses the maximum inner product search to retrieve Wikipedia articles relevant to a particular query or question. The model was fine-tuned for factoid-based question answering on the Natural Questions dataset. REALM utilizes the BERT model to learn good representations for a question and uses SCANN to retrieve Wikipedia articles that have a high topical similarity with the question representation. This is then trained end-to-end to maximize the log-likelihood on the QA task.

We further improve the quality of REALM retrievals by using a contrastive loss. The idea behind this is to encourage the representation of a question to get close to its ground truth answer and diverge from the other answers in its mini-batch. This ensures that when the system retrieves relevant items using this question representation, it returns articles that are “similar” to ground truth answers. We call this retriever contrastive-REALM or c-REALM.

The combined RT + c-REALM system for LFQA.

Evaluation
We test the model on long-form question answering using the ELI5 dataset, which is a part of the KILT benchmark, and is the only publicly available large-scale LFQA dataset. The KILT benchmark measures text retrievals using Precision (R-Prec) and text generation using ROUGE-L. The two scores are combined to give a KILT R-L score, which determines a model’s ranking on the leaderboard. We fine-tune the pre-trained RT model together with retrievals from c-REALM on the ELI5 dataset from KILT.

Our submission tops the KILT leaderboard for long-form question answering on ELI5 with a combined KILT R-L score of 2.36. It improves on the previous leaderboard entry of BART + DPR (KILT R-L score of 1.9), while having a similar number of parameters as the other models on the leaderboard. In terms of text generation quality, we see an improvement of +4.11, +5.78 and +9.14 Rouge-L over T5, BART + DPR and RAG, respectively.

Our results on the KILT leaderboard for long form question answering on ELI5.

Example Generations from the RT Model

• 1
  Q: Why are almost all boats white?

  Boats are generally painted white for obvious reasons, as they are inexpensive and easy to clean. Ships are also often painted to provide a visible visual contrast to the sea. Boats also often have high visibility ports to allow for easy international trade. In addition, many boats have an air-breathing function that makes them easier to spot and stay afloat, which is a good thing if you’re a pirate or trying to get into some country’s waters. Lastly, many ships are built in the last few decades, so they are not as exotic looking as they were thirty years ago. And lastly, many ships are made out of materials that are easy to work with, and so many of them are painted white as a practical matter. There are many, many more reasons for why ships are white, but those are the ones I know of. I’m sure there are many other reasons, but those are the ones I know of. Edit: I forgot to mention that the other answers about visibility and easy to see ports are also true. Ships are painted to appear to be larger, and more expensive. That makes them appear more impressive, and so they are more likely to be bought by people who want to show off their wealth and status.

• 2
  Q: What causes the trail behind jets at high altitude?

  The same thing that causes the clouds you see at the start of a storm to form in the first place. The air pressure changes as the jet moves through the air, causing it to cool down and condense into water droplets. These droplets are in fact a lot bigger than the water droplets in the clouds, so when the plane passes through them, they can cause the air pressure to change, causing the water droplets to condense into clouds. This is what you see when you look at a cloud formation from the ground. In addition to this, when the plane passes through the clouds, it also moves through the air, causing it to change its temperature, causing the water droplets to condense and form clouds. These clouds are often quite large, and can block out the sun. This is what you see when you look at a contrail. Finally, the water vapor that forms at high altitudes is cooled by the air above, and as it cools, it condenses into clouds. This is what you see when you look at a cumulonimbus cloud. These clouds are even larger than the water droplets in the clouds, and they block out the sun.

• 3
  Q: How do shampoo and conditioner work?

  The key ingredients in shampoo and conditioner are usually surfactants, they tend to attract oil from your skin. Shampoo will usually contain an anti-dandruff agent (dandruff is caused by fungi in your skin which cause dandruff). They also contain some moisturizing agents (moisturizers are things that stay in your skin longer and protect your scalp from cleaning), and a lot of anti-dandruff (dandruff is a side effect of high doses of both surfactants and moisturizers) Conditioner will contain moisturizing agents, like a skin moisturizer. They tend to cause oils to be separated from your hair (e.g. wash your hair with conditioner instead of shampoo). They both have a foaming agent that makes them foam up (usually Hydrogen Peroxide). They also have a foaming agent that stops dirt from attaching to your hair. Some conditioner will also suppress the action of the shampoo (to help prevent dirt from attaching to your hair).

• 4
  Q: When glancing at a clock, why does the first second after glancing at it sometimes feel longer than the rest?

  This is known as chronostasis. Your brain gets used to seeing the second hand move after the first, so it ignores the first one. If you were to look at the clock a lot, you’d see the second hand move a lot more than the first, and you’d be able to tell the difference between the second and the first. The second hand will appear to move much slower than the first hand because your brain is used to seeing the second hand move a lot more than the first. If you were to go on a long trip, you’d get used to the second hand moving a lot more than the first, and you’d have no problem telling the difference between the second and the first hand. It’s kind of like how you don’t notice your nose when you’re driving, but if you look at it for a while, you start to notice it. Your brain is just getting used to seeing the nose move a lot more than the other, and it can’t tell the difference between the two. It’s kind of like that with your eyes.

• 5
  Q: Why do Britain and other English empire countries still bow to monarchs? What real purpose does the queen serve?

  Depends what you define as “purpose”. There is no specific purpose for the British monarch – rather, they are figureheads that serve a role. The role is to have a high degree of influence over a country, though the rules of the monarchy can somewhat vary from country to country, and the ceremony of “kissing the royal corpse” does not always involve kissing the monarch. Whether that’s the only reason for the custom, or if it was the only reason, I can’t say, but that’s the reasoning. When the U.K. was in full power, the monarch was a puppet of Parliament, and the powers of the monarch were transferred to the Prime Minister and thus to the Prime Minister’s deputy, who then became the Prime Minister. Since then, Parliament has been able to vote on legislation that goes through the monarch, although they may still act as the monarch’s representative in negotiating treaties, which can have very very deep consequences. The Queen’s role, as a representative of Britain, doesn’t necessarily involve her formal approval of any of the laws or legislation that goes through Parliament, though.

• 6
  Q: What exactly is fire, in detail? How can light and heat come from something we can’t really touch?

  Fire is the chemical reaction of fuel (oxygen) with (what we call) impurities (ash, soot, oil etc). These impurities are created due to a number of things. If you were to study the chemical composition of a log (or a candle) and analyse it you would discover the chemical formula (A, C, and G) which is a simplified version of what actually happens. There is always fuel, and there is always the ash/soot. Wood is made up of mostly carbon and hydrogen and these are the fuels that create the fire. Hydrogen and oxygen are reactive, and they form water (H2O) and CO2 (CO2). If we split a log into smaller pieces, we start to see the process of combustion as it occurs. The carbon is burned, and with the explosion of CO, H2O and H2CO2, we get water and carbon dioxide (mostly). If we smash a log together, we start to see what happens when we also hit another log with another log…imagine smashing two sand castles together. We see how the sand castles and brick castles form and collapse at different rates…then it starts to burn. The smoke, ash and flames are the actual combustion of fuel.

• 7
  Q: What goes on in those tall tower buildings owned by major banks?

  The actual buildings are not there for profit but for show. There are many real world historical buildings that have little to no effect other than being a symbol of an economic entity or symbol of an era or location, and nothing more. For example look at Sears, Sears didn’t care what went on inside, it was all about the _appearance_ of its location, the prestige of the location, the facilities and so on. It didn’t care about how long it took it to operate, it was about how much people would pay to go see it. Sears was a landmark as a cultural movement and other big companies followed suit, so if you want to see a building you’ve never seen before, you have to go see Sears, just like you have to see a Toyota Camry for Toyota Camry. They used to be all about building new factories, some of them if I recall, but now that they’re bigger, that means that more factory jobs are coming to them. You’ve probably seen them in stores as stores where people buy and sell stuff, so there aren’t that many places for them to come from. Instead, it’s just for show, a symbol of rich people.

Hurdles Towards Progress in LFQA
However, while the RT system described here tops the public leaderboard, a detailed analysis of the model and the ELI5 dataset reveal some concerning trends.

• Train/Valid Overlap
  Many held-out questions are paraphrased in the training set. Best answer to similar train questions gets 27.4 ROUGE-L.

  

• Gaming ROUGE-L
  Simply retrieving answers to random unrelated training questions yields relatively high ROUGE-L, while actual gold answers underperform generations.

  

• Lack of Grounding
  Conditioning answer generation on random documents instead of relevant ones does not measurably impact its factual correctness. Longer outputs get higher ROUGE-L.

  

We find little to no evidence that the model is actually grounding its text generation in the retrieved documents — fine-tuning an RT model with random retrievals from Wikipedia (i.e., random retrieval + RT) performs nearly as well as the c-REALM + RT model (24.2 vs 24.4 ROUGE-L). We also find significant overlap in the training, validation and test sets of ELI5 (with several questions being paraphrases of each other), which may eliminate the need for retrievals. The KILT benchmark measures the quality of retrievals and generations separately, without making sure that the text generation actually use the retrievals.

Trivial baselines get higher Rouge-L scores than RAG and BART + DPR.

Moreover, we find issues with the Rouge-L metric used to evaluate the quality of text generation, with trivial nonsensical baselines, such as a Random Training Set answer and Input Copying, achieving relatively high Rouge-L scores (even beating BART + DPR and RAG).

Conclusion
We proposed a system for long form-question answering based on Routing Transformers and REALM, which tops the KILT leaderboard on ELI5. However, a detailed analysis reveals several issues with the benchmark that preclude using it to inform meaningful modelling advances. We hope that the community works together to solve these issues so that researchers can climb the right hills and make meaningful progress in this challenging but important task.

Acknowledgments
The Routing Transformer work has been a team effort involving Aurko Roy, Mohammad Saffar, Ashish Vaswani and David Grangier. The follow-up work on open-domain long-form question answering has been a collaboration involving Kalpesh Krishna, Aurko Roy and Mohit Iyyer. We wish to thank Vidhisha Balachandran, Niki Parmar and Ashish Vaswani for several helpful discussions, and the REALM team (Kenton Lee, Kelvin Guu, Ming-Wei Chang and Zora Tung) for help with their codebase and several useful discussions, which helped us improve our experiments. We are grateful to Tu Vu for help with the QQP classifier used to detect paraphrases in ELI5 train and test sets. We thank Jules Gagnon-Marchand and Sewon Min for suggesting useful experiments on checking ROUGE-L bounds. Finally we thank Shufan Wang, Andrew Drozdov, Nader Akoury and the rest of the UMass NLP group for helpful discussions and suggestions at various stages in the project.

Posted by Ji Hun Kim and Richard Wu, Software Engineers, Stadia

Over the years, online multiplayer games have exploded in popularity, captivating millions of players across the world. This popularity has also exponentially increased demands on game designers, as players expect games to be well-crafted and balanced — after all, it’s no fun to play a game where a single strategy beats all the rest.

In order to create a positive gameplay experience, game designers typically tune the balance of a game iteratively:

1. Stress-test through thousands of play-testing sessions from test users
2. Incorporate feedback and re-design the game
3. Repeat 1 & 2 until both the play-testers and game designers are satisfied

This process is not only time-consuming but also imperfect — the more complex the game, the easier it is for subtle flaws to slip through the cracks. When games often have many different roles that can be played, with dozens of interconnecting skills, it makes it all the more difficult to hit the right balance.

Today, we present an approach that leverages machine learning (ML) to adjust game balance by training models to serve as play-testers, and demonstrate this approach on the digital card game prototype Chimera, which we’ve previously shown as a testbed for ML-generated art. By running millions of simulations using trained agents to collect data, this ML-based game testing approach enables game designers to more efficiently make a game more fun, balanced, and aligned with their original vision.

Chimera
We developed Chimera as a game prototype that would heavily lean on machine learning during its development process. For the game itself, we purposefully designed the rules to expand the possibility space, making it difficult to build a traditional hand-crafted AI to play the game.

The gameplay of Chimera revolves around the titular chimeras, creature mash-ups that players aim to strengthen and evolve. The objective of the game is to defeat the opponent’s chimera. These are the key points in the game design:

• Players may play:
  • creatures, which can attack (through their attack stat) or be attacked (against their health stat), or
  • spells, which produce special effects.
• Creatures are summoned into limited-capacity biomes, which are placed physically on the board space. Each creature has a preferred biome and will take repeated damage if placed on an incorrect biome or a biome that is over capacity.
• A player controls a single chimera, which starts off in a basic “egg” state and can be evolved and strengthened by absorbing creatures. To do this, the player must also acquire a certain amount of link energy, which is generated from various gameplay mechanics.
• The game ends when a player has successfully brought the health of the opponent’s chimera to 0.

Learning to Play Chimera
As an imperfect information card game with a large state space, we expected Chimera to be a difficult game for an ML model to learn, especially as we were aiming for a relatively simple model. We used an approach inspired by those used by earlier game-playing agents like AlphaGo, in which a convolutional neural network (CNN) is trained to predict the probability of a win when given an arbitrary game state. After training an initial model on games where random moves were chosen, we set the agent to play against itself, iteratively collecting game data, that was then used to train a new agent. With each iteration, the quality of the training data improved, as did the agent’s ability to play the game.

The ML agent’s performance against our best hand-crafted AI as training progressed. The initial ML agent (version 0) picked moves randomly.

For the actual game state representation that the model would receive as input, we found that passing an “image” encoding to the CNN resulted in the best performance, beating all benchmark procedural agents and other types of networks (e.g. fully connected). The chosen model architecture is small enough to run on a CPU in reasonable time, which allowed us to download the model weights and run the agent live in a Chimera game client using Unity Barracuda.

An example game state representation used to train the neural network.

In addition to making decisions for the game AI, we also used the model to display the estimated win probability for a player over the course of the game.

Balancing Chimera
This approach enabled us to simulate millions more games than real players would be capable of playing in the same time span. After collecting data from the games played by the best-performing agents, we analyzed the results to find imbalances between the two of the player decks we had designed.

First, the Evasion Link Gen deck was composed of spells and creatures with abilities that generated extra link energy used to evolve a player’s chimera. It also contained spells that enabled creatures to evade attacks. In contrast, the Damage-Heal deck contained creatures of variable strength with spells that focused on healing and inflicting minor damage. Although we had designed these decks to be of equal strength, the Evasion Link Gen deck was winning 60% of the time when played against the Damage-Heal deck.

When we collected various stats related to biomes, creatures, spells, and chimera evolutions, two things immediately jumped out at us:

1. There was a clear advantage in evolving a chimera — the agent won a majority of the games where it evolved its chimera more than the opponent did. Yet, the average number of evolves per game did not meet our expectations. To make it more of a core game mechanic, we wanted to increase the overall average number of evolves while keeping its usage strategic.
2. The T-Rex creature was overpowered. Its appearances correlated strongly with wins, and the model would always play the T-Rex regardless of penalties for summoning into an incorrect or overcrowded biome.

From these insights, we made some adjustments to the game. To emphasize chimera evolution as a core mechanism in the game, we decreased the amount of link energy required to evolve a chimera from 3 to 1. We also added a “cool-off” period to the T-Rex creature, doubling the time it took to recover from any of its actions.

Repeating our ‘self-play’ training procedure with the updated rules, we observed that these changes pushed the game in the desired direction — the average number of evolves per game increased, and the T-Rex’s dominance faded.

One example comparison of the T-Rex’s influence before and after balancing. The charts present the number of games won (or lost) when a deck initiates a particular spell interaction (e.g., using the “Dodge” spell to benefit a T-Rex). Left: Before the changes, the T-Rex had a strong influence in every metric examined — highest survival rate, most likely to be summoned ignoring penalties, most absorbed creature during wins. Right: After the changes, the T-Rex was much less overpowered.

By weakening the T-Rex, we successfully reduced the Evasion Link Gen deck’s reliance on an overpowered creature. Even so, the win ratio between the decks remained at 60/40 rather than 50/50. A closer look at the individual game logs revealed that the gameplay was often less strategic than we would have liked. Searching through our gathered data again, we found several more areas to introduce changes in.

To start, we increased the starting health of both players as well as the amount of health that healing spells could replenish. This was to encourage longer games that would allow a more diverse set of strategies to flourish. In particular, this enabled the Damage-Heal deck to survive long enough to take advantage of its healing strategy. To encourage proper summoning and strategic biome placement, we increased the existing penalties on playing creatures into incorrect or overcrowded biomes. And finally, we decreased the gap between the strongest and weakest creatures through minor attribute adjustments.

New adjustments in place, we arrived at the final game balance stats for these two decks:

Conclusion
Normally, identifying imbalances in a newly prototyped game can take months of playtesting. With this approach, we were able to not only discover potential imbalances but also introduce tweaks to mitigate them in a span of days. We found that a relatively simple neural network was sufficient to reach high level performance against humans and traditional game AI. These agents could be leveraged in further ways, such as for coaching new players or discovering unexpected strategies. We hope this work will inspire more exploration in the possibilities of machine learning for game development.

Acknowledgements
This project was conducted in collaboration with many people. Thanks to Ryan Poplin, Maxwell Hannaman, Taylor Steil, Adam Prins, Michal Todorovic, Xuefan Zhou, Aaron Cammarata, Andeep Toor, Trung Le, Erin Hoffman-John, and Colin Boswell. Thanks to everyone who contributed through playtesting, advising on game design, and giving valuable feedback.

This is the final post in a four-part introduction to time-series forecasting with torch. These posts have been the story of a quest for multiple-step prediction, and by now, we’ve seen three different approaches: forecasting in a loop, incorporating a multi-layer perceptron (MLP), and sequence-to-sequence models. Here’s a quick recap.

• As one should when one sets out for an adventurous journey, we started with an in-depth study of the tools at our disposal: recurrent neural networks (RNNs). We trained a model to predict the very next observation in line, and then, thought of a clever hack: How about we use this for multi-step prediction, feeding back individual predictions in a loop? The result , it turned out, was quite acceptable.

• Then, the adventure really started. We built our first model “natively” for multi-step prediction, relieving the RNN a bit of its workload and involving a second player, a tiny-ish MLP. Now, it was the MLP’s task to project RNN output to several time points in the future. Although results were pretty satisfactory, we didn’t stop there.

• Instead, we applied to numerical time series a technique commonly used in natural language processing (NLP): sequence-to-sequence (seq2seq) prediction. While forecast performance was not much different from the previous case, we found the technique to be more intuitively appealing, since it reflects the causal relationship between successive forecasts.

Today we’ll enrich the seq2seq approach by adding a new component: the attention module. Originally introduced around 20141, attention mechanisms have gained enormous traction, so much so that a recent paper title starts out “Attention is Not All You Need”2.

The idea is the following.

In the classic encoder-decoder setup, the decoder gets “primed” with an encoder summary just a single time: the time it starts its forecasting loop. From then on, it’s on its own. With attention, however, it gets to see the complete sequence of encoder outputs again every time it forecasts a new value. What’s more, every time, it gets to zoom in on those outputs that seem relevant for the current prediction step.

This is a particularly useful strategy in translation: In generating the next word, a model will need to know what part of the source sentence to focus on. How much the technique helps with numerical sequences, in contrast, will likely depend on the features of the series in question.

Data input

As before, we work with vic_elec, but this time, we partly deviate from the way we used to employ it. With the original, bi-hourly dataset, training the current model takes a long time, longer than readers will want to wait when experimenting. So instead, we aggregate observations by day. In order to have enough data, we train on years 2012 and 2013, reserving 2014 for validation as well as post-training inspection.

vic_elec_daily <- vic_elec %>%
  select(Time, Demand) %>%
  index_by(Date = date(Time)) %>%
  summarise(
    Demand = sum(Demand) / 1e3) 

elec_train <- vic_elec_daily %>% 
  filter(year(Date) %in% c(2012, 2013)) %>%
  as_tibble() %>%
  select(Demand) %>%
  as.matrix()

elec_valid <- vic_elec_daily %>% 
  filter(year(Date) == 2014) %>%
  as_tibble() %>%
  select(Demand) %>%
  as.matrix()

elec_test <- vic_elec_daily %>% 
  filter(year(Date) %in% c(2014), month(Date) %in% 1:4) %>%
  as_tibble() %>%
  select(Demand) %>%
  as.matrix()

train_mean <- mean(elec_train)
train_sd <- sd(elec_train)

We’ll attempt to forecast demand up to fourteen days ahead. How long, then, should be the input sequences? This is a matter of experimentation; all the more so now that we’re adding in the attention mechanism. (I suspect that it might not handle very long sequences so well).

Below, we go with fourteen days for input length, too, but that may not necessarily be the best possible choice for this series.

n_timesteps <- 7 * 2
n_forecast <- 7 * 2

elec_dataset <- dataset(
  name = "elec_dataset",
  
  initialize = function(x, n_timesteps, sample_frac = 1) {
    
    self$n_timesteps <- n_timesteps
    self$x <- torch_tensor((x - train_mean) / train_sd)
    
    n <- length(self$x) - self$n_timesteps - 1
    
    self$starts <- sort(sample.int(
      n = n,
      size = n * sample_frac
    ))
    
  },
  
  .getitem = function(i) {
    
    start <- self$starts[i]
    end <- start + self$n_timesteps - 1
    lag <- 1
    
    list(
      x = self$x[start:end],
      y = self$x[(start+lag):(end+lag)]$squeeze(2)
    )
    
  },
  
  .length = function() {
    length(self$starts) 
  }
)

batch_size <- 32

train_ds <- elec_dataset(elec_train, n_timesteps, sample_frac = 0.5)
train_dl <- train_ds %>% dataloader(batch_size = batch_size, shuffle = TRUE)

valid_ds <- elec_dataset(elec_valid, n_timesteps, sample_frac = 0.5)
valid_dl <- valid_ds %>% dataloader(batch_size = batch_size)

test_ds <- elec_dataset(elec_test, n_timesteps)
test_dl <- test_ds %>% dataloader(batch_size = 1)

Model

Model-wise, we again encounter the three modules familiar from the previous post: encoder, decoder, and top-level seq2seq module. However, there is an additional component: the attention module, used by the decoder to obtain attention weights.

Encoder

The encoder still works the same way. It wraps an RNN, and returns the final state.

encoder_module <- nn_module(
  
  initialize = function(type, input_size, hidden_size, num_layers = 1, dropout = 0) {
    
    self$type <- type
    
    self$rnn <- if (self$type == "gru") {
      nn_gru(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        dropout = dropout,
        batch_first = TRUE
      )
    } else {
      nn_lstm(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        dropout = dropout,
        batch_first = TRUE
      )
    }
    
  },
  
  forward = function(x) {
    
    x <- self$rnn(x)
    
    # return last states for all layers
    # per layer, a single tensor for GRU, a list of 2 tensors for LSTM
    x <- x[[2]]
    x
    
  }
)

Attention module

In basic seq2seq, whenever it had to generate a new value, the decoder took into account two things: its prior state, and the previous output generated. In an attention-enriched setup, the decoder additionally receives the complete output from the encoder. In deciding what subset of that output should matter, it gets help from a new agent, the attention module.

This, then, is the attention module’s raison d’être: Given current decoder state and well as complete encoder outputs, obtain a weighting of those outputs indicative of how relevant they are to what the decoder is currently up to. This procedure results in the so-called attention weights: a normalized score, for each time step in the encoding, that quantify their respective importance.

Attention may be implemented in a number of different ways. Here, we show two implementation options, one additive, and one multiplicative.

Additive attention

In additive attention, encoder outputs and decoder state are commonly either added or concatenated (we choose to do the latter, below). The resulting tensor is run through a linear layer, and a softmax is applied for normalization.

attention_module_additive <- nn_module(
  
  initialize = function(hidden_dim, attention_size) {
    
    self$attention <- nn_linear(2 * hidden_dim, attention_size)
    
  },
  
  forward = function(state, encoder_outputs) {
    
    # function argument shapes
    # encoder_outputs: (bs, timesteps, hidden_dim)
    # state: (1, bs, hidden_dim)
    
    # multiplex state to allow for concatenation (dimensions 1 and 2 must agree)
    seq_len <- dim(encoder_outputs)[2]
    # resulting shape: (bs, timesteps, hidden_dim)
    state_rep <- state$permute(c(2, 1, 3))$repeat_interleave(seq_len, 2)
    
    # concatenate along feature dimension
    concat <- torch_cat(list(state_rep, encoder_outputs), dim = 3)
    
    # run through linear layer with tanh
    # resulting shape: (bs, timesteps, attention_size)
    scores <- self$attention(concat) %>% 
      torch_tanh()
    
    # sum over attention dimension and normalize
    # resulting shape: (bs, timesteps) 
    attention_weights <- scores %>%
      torch_sum(dim = 3) %>%
      nnf_softmax(dim = 2)
    
    # a normalized score for every source token
    attention_weights
  }
)

Multiplicative attention

In multiplicative attention, scores are obtained by computing dot products between decoder state and all of the encoder outputs. Here too, a softmax is then used for normalization.

attention_module_multiplicative <- nn_module(
  
  initialize = function() {
    
    NULL
    
  },
  
  forward = function(state, encoder_outputs) {
    
    # function argument shapes
    # encoder_outputs: (bs, timesteps, hidden_dim)
    # state: (1, bs, hidden_dim)

    # allow for matrix multiplication with encoder_outputs
    state <- state$permute(c(2, 3, 1))
 
    # prepare for scaling by number of features
    d <- torch_tensor(dim(encoder_outputs)[3], dtype = torch_float())
       
    # scaled dot products between state and outputs
    # resulting shape: (bs, timesteps, 1)
    scores <- torch_bmm(encoder_outputs, state) %>%
      torch_div(torch_sqrt(d))
    
    # normalize
    # resulting shape: (bs, timesteps) 
    attention_weights <- scores$squeeze(3) %>%
      nnf_softmax(dim = 2)
    
    # a normalized score for every source token
    attention_weights
  }
)

Decoder

Once attention weights have been computed, their actual application is handled by the decoder. Concretely, the method in question, weighted_encoder_outputs(), computes a product of weights and encoder outputs, making sure that each output will have appropriate impact.

The rest of the action then happens in forward(). A concatenation of weighted encoder outputs (often called “context”) and current input is run through an RNN. Then, an ensemble of RNN output, context, and input is passed to an MLP. Finally, both RNN state and current prediction are returned.

decoder_module <- nn_module(
  
  initialize = function(type, input_size, hidden_size, attention_type, attention_size = 8, num_layers = 1) {
    
    self$type <- type
    
    self$rnn <- if (self$type == "gru") {
      nn_gru(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        batch_first = TRUE
      )
    } else {
      nn_lstm(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        batch_first = TRUE
      )
    }
    
    self$linear <- nn_linear(2 * hidden_size + 1, 1)
    
    self$attention <- if (attention_type == "multiplicative") attention_module_multiplicative()
      else attention_module_additive(hidden_size, attention_size)
    
  },
  
  weighted_encoder_outputs = function(state, encoder_outputs) {

    # encoder_outputs is (bs, timesteps, hidden_dim)
    # state is (1, bs, hidden_dim)
    # resulting shape: (bs * timesteps)
    attention_weights <- self$attention(state, encoder_outputs)
    
    # resulting shape: (bs, 1, seq_len)
    attention_weights <- attention_weights$unsqueeze(2)
    
    # resulting shape: (bs, 1, hidden_size)
    weighted_encoder_outputs <- torch_bmm(attention_weights, encoder_outputs)
    
    weighted_encoder_outputs
    
  },
  
  forward = function(x, state, encoder_outputs) {
 
    # encoder_outputs is (bs, timesteps, hidden_dim)
    # state is (1, bs, hidden_dim)
    
    # resulting shape: (bs, 1, hidden_size)
    context <- self$weighted_encoder_outputs(state, encoder_outputs)
    
    # concatenate input and context
    # NOTE: this repeating is done to compensate for the absence of an embedding module
    # that, in NLP, would give x a higher proportion in the concatenation
    x_rep <- x$repeat_interleave(dim(context)[3], 3) 
    rnn_input <- torch_cat(list(x_rep, context), dim = 3)
    
    # resulting shapes: (bs, 1, hidden_size) and (1, bs, hidden_size)
    rnn_out <- self$rnn(rnn_input, state)
    rnn_output <- rnn_out[[1]]
    next_hidden <- rnn_out[[2]]
    
    mlp_input <- torch_cat(list(rnn_output$squeeze(2), context$squeeze(2), x$squeeze(2)), dim = 2)
    
    output <- self$linear(mlp_input)
    
    # shapes: (bs, 1) and (1, bs, hidden_size)
    list(output, next_hidden)
  }
  
)

seq2seq module

The seq2seq module is basically unchanged (apart from the fact that now, it allows for attention module configuration). For a detailed explanation of what happens here, please consult the previous post.

seq2seq_module <- nn_module(
  
  initialize = function(type, input_size, hidden_size, attention_type, attention_size, n_forecast, 
                        num_layers = 1, encoder_dropout = 0) {
    
    self$encoder <- encoder_module(type = type, input_size = input_size, hidden_size = hidden_size,
                                   num_layers, encoder_dropout)
    self$decoder <- decoder_module(type = type, input_size = 2 * hidden_size, hidden_size = hidden_size,
                                   attention_type = attention_type, attention_size = attention_size, num_layers)
    self$n_forecast <- n_forecast
    
  },
  
  forward = function(x, y, teacher_forcing_ratio) {
    
    outputs <- torch_zeros(dim(x)[1], self$n_forecast)$to(device = device)
    encoded <- self$encoder(x)
    encoder_outputs <- encoded[[1]]
    hidden <- encoded[[2]]
    # list of (batch_size, 1), (1, batch_size, hidden_size)
    out <- self$decoder(x[ , n_timesteps, , drop = FALSE], hidden, encoder_outputs)
    # (batch_size, 1)
    pred <- out[[1]]
    # (1, batch_size, hidden_size)
    state <- out[[2]]
    outputs[ , 1] <- pred$squeeze(2)
    
    for (t in 2:self$n_forecast) {
      
      teacher_forcing <- runif(1) < teacher_forcing_ratio
      input <- if (teacher_forcing == TRUE) pred$unsqueeze(3) else y[ , t - 1]
      out <- self$decoder(pred$unsqueeze(3), state, encoder_outputs)
      pred <- out[[1]]
      state <- out[[2]]
      outputs[ , t] <- pred$squeeze(2)
      
    }
    
    outputs
  }
  
)

When instantiating the top-level model, we now have an additional choice: that between additive and multiplicative attention. In the “accuracy” sense of performance, my tests did not show any differences. However, the multiplicative variant is a lot faster.

net <- seq2seq_module("gru", input_size = 1, hidden_size = 32, attention_type = "multiplicative",
                      attention_size = 8, n_forecast = n_timesteps)

# training RNNs on the GPU currently prints a warning that may clutter 
# the console
# see https://github.com/mlverse/torch/issues/461
# alternatively, use 
# device <- "cpu"
device <- torch_device(if (cuda_is_available()) "cuda" else "cpu")

net <- net$to(device = device)

Training

Just like last time, in model training, we get to choose the degree of teacher forcing. Below, we go with a fraction of 0.0, that is, no forcing at all.

optimizer <- optim_adam(net$parameters, lr = 0.001)

num_epochs <- 100

train_batch <- function(b, teacher_forcing_ratio) {
  
  optimizer$zero_grad()
  output <- net(b$x$to(device = device), b$y$to(device = device), teacher_forcing_ratio)
  target <- b$y$to(device = device)
  
  loss <- nnf_mse_loss(output, target)
  loss$backward()
  optimizer$step()
  
  loss$item()
  
}

valid_batch <- function(b, teacher_forcing_ratio = 0) {
  
  output <- net(b$x$to(device = device), b$y$to(device = device), teacher_forcing_ratio)
  target <- b$y$to(device = device)
  
  loss <- nnf_mse_loss(output, target)
  
  loss$item()
  
}

for (epoch in 1:num_epochs) {
  
  net$train()
  train_loss <- c()
  
  coro::loop(for (b in train_dl) {
    loss <-train_batch(b, teacher_forcing_ratio = 0.3)
    train_loss <- c(train_loss, loss)
  })
  
  cat(sprintf("nEpoch %d, training: loss: %3.5f n", epoch, mean(train_loss)))
  
  net$eval()
  valid_loss <- c()
  
  coro::loop(for (b in valid_dl) {
    loss <- valid_batch(b)
    valid_loss <- c(valid_loss, loss)
  })
  
  cat(sprintf("nEpoch %d, validation: loss: %3.5f n", epoch, mean(valid_loss)))
}

# Epoch 1, training: loss: 0.83752 
# Epoch 1, validation: loss: 0.83167

# Epoch 2, training: loss: 0.72803 
# Epoch 2, validation: loss: 0.80804 

# ...
# ...

# Epoch 99, training: loss: 0.10385 
# Epoch 99, validation: loss: 0.21259 

# Epoch 100, training: loss: 0.10396 
# Epoch 100, validation: loss: 0.20975 

Evaluation

For visual inspection, we pick a few forecasts from the test set.

net$eval()

test_preds <- vector(mode = "list", length = length(test_dl))

i <- 1

vic_elec_test <- vic_elec_daily %>%
  filter(year(Date) == 2014, month(Date) %in% 1:4)


coro::loop(for (b in test_dl) {
  
  input <- b$x
  output <- net(b$x$to(device = device), b$y$to(device = device), teacher_forcing_ratio = 0)
  preds <- as.numeric(output)
  
  test_preds[[i]] <- preds
  i <<- i + 1
  
})

test_pred1 <- test_preds[[1]]
test_pred1 <- c(rep(NA, n_timesteps), test_pred1, rep(NA, nrow(vic_elec_test) - n_timesteps - n_forecast))

test_pred2 <- test_preds[[21]]
test_pred2 <- c(rep(NA, n_timesteps + 20), test_pred2, rep(NA, nrow(vic_elec_test) - 20 - n_timesteps - n_forecast))

test_pred3 <- test_preds[[41]]
test_pred3 <- c(rep(NA, n_timesteps + 40), test_pred3, rep(NA, nrow(vic_elec_test) - 40 - n_timesteps - n_forecast))

test_pred4 <- test_preds[[61]]
test_pred4 <- c(rep(NA, n_timesteps + 60), test_pred4, rep(NA, nrow(vic_elec_test) - 60 - n_timesteps - n_forecast))

test_pred5 <- test_preds[[81]]
test_pred5 <- c(rep(NA, n_timesteps + 80), test_pred5, rep(NA, nrow(vic_elec_test) - 80 - n_timesteps - n_forecast))


preds_ts <- vic_elec_test %>%
  select(Demand, Date) %>%
  add_column(
    ex_1 = test_pred1 * train_sd + train_mean,
    ex_2 = test_pred2 * train_sd + train_mean,
    ex_3 = test_pred3 * train_sd + train_mean,
    ex_4 = test_pred4 * train_sd + train_mean,
    ex_5 = test_pred5 * train_sd + train_mean) %>%
  pivot_longer(-Date) %>%
  update_tsibble(key = name)


preds_ts %>%
  autoplot() +
  scale_color_hue(h = c(80, 300), l = 70) +
  theme_minimal()

(#fig:unnamed-chunk-11)A sample of two-weeks-ahead predictions for the test set, 2014.

We can’t directly compare performance here to that of previous models in our series, as we’ve pragmatically redefined the task. The main goal, however, has been to introduce the concept of attention. Specifically, how to manually implement the technique – something that, once you’ve understood the concept, you may never have to do in practice. Instead, you would likely make use of existing tools that come with torch (multi-head attention and transformer modules), tools we may introduce in a future “season” of this series.

Thanks for reading!

Photo by David Clode on Unsplash

Posted by Jakub Łącki and Vahab Mirrokni, Research Scientists, Google Research

Graphs are useful theoretical representations of the connections between groups of entities, and have been used for a variety of purposes in data science, from ranking web pages by popularity and mapping out social networks, to assisting with navigation. In many cases, such applications require the processing of graphs containing hundreds of billions of edges, which is far too large to be processed on a single consumer-grade machine. A typical approach to scaling graph algorithms is to run in a distributed setting, i.e., to partition the data (and the algorithm) among multiple computers to perform the computation in parallel. While this approach allows one to process graphs with trillions of edges, it also introduces new challenges. Namely, because each computer only sees a small piece of the input graph at a time, one needs to handle inter-machine communication and design algorithms that can be split across multiple computers.

A framework for implementing distributed algorithms, MapReduce, was introduced in 2008. It transparently handled communication between machines while offering good fault-tolerance capabilities and inspired the development of a number of distributed computation frameworks, including Pregel, Apache Hadoop, and many others. Still, the challenge of developing algorithms for distributed computation on very large graphs remained, and designing efficient algorithms in this context even for basic problems, such as connected components, maximum matching or shortest paths, has been an active area of research. While recent work has demonstrated new algorithms for many problems, including our algorithms for connected components (both in theory and practice) and hierarchical clustering, there was still a need for methods that could solve a range of problems more quickly.

Today we present a pair of recent papers that address this problem by first constructing a theoretical model for distributed graph algorithms and then demonstrating how the model can be applied. The proposed model, Adaptive Massively Parallel Computation (AMPC), augments the theoretical capabilities of MapReduce, providing a pathway to solve many graph problems in fewer computation rounds. We also show how the AMPC model can be effectively implemented in practice. The suite of algorithms we describe, which includes algorithms for maximal independent set, maximum matching, connected components and minimum spanning tree, work up to 7x faster than current state-of-the-art approaches.

Limitations of MapReduce
In order to understand the limitations of MapReduce for developing graph algorithms, consider a simplified variant of the connected components problem. The input is a collection of rooted trees, and the goal is to compute, for each node, the root of its tree. Even this seemingly simple problem is not easy to solve in MapReduce. In fact, in the Massively Parallel Computation (MPC) model — the theoretical model behind MapReduce, Pregel, Apache Giraph and many other distributed computation frameworks — this problem is widely believed to require at least a number of rounds of computation proportional to log n, where n is the total number of nodes in the graph. While log n may not seem to be a large number, algorithms processing trillion-edge graphs often write hundreds of terabytes of data to disk in each round, and thus even a small reduction in the number of rounds may bring significant resource savings.

The problem of finding root nodes. Nodes are represented by blue circles. Gray arrows point from each node to its parent. The root nodes are the nodes with no parents. The orange arrows illustrate the path an algorithm would follow from a node to the root of the tree to which it belongs.

A similar subproblem showed up in our algorithms for finding connected components and computing a hierarchical clustering. We observed that one can bypass the limitations of MapReduce by implementing these algorithms through the use of a distributed hash table (DHT), a service that is initialized with a collection of key-value pairs and then returns a value associated with a provided key in real-time. In our implementation, for each node, the DHT stores its parent node. Then, a machine that processes a graph node can use the DHT and “walk up” the tree until it reaches the root. While the use of a DHT worked well for this particular problem (although it relied on the input trees being not too deep), it was unclear if the idea could be applied more broadly.

The Adaptive Massively Parallel Computation Model
To extend this approach to other problems, we started by developing a model to theoretically analyze algorithms that utilize a DHT. The resulting AMPC model builds upon the well-established MPC model and formally describes the capabilities brought by the use of a distributed hash table.

In the MPC model there is a collection of machines, which communicate via message passing in synchronous rounds. Messages sent in one round are delivered in the beginning of the following round and constitute that round’s entire input (i.e., the machines do not retain information from one round to the next). In the first round, one can assume that the input is randomly distributed across the machines. The goal is to minimize the number of computation rounds, while assuring load-balancing between machines in each round.

Computation in the MPC model. Each column represents one machine in subsequent computation rounds. Once all machines have completed a round of computation, all messages sent in that round are delivered, and the following round begins.

We then formalized the AMPC model by introducing a new approach, in which machines write to a write-only distributed hash table each round, instead of communicating via messages. Once a new round starts, the hash table from the previous round becomes read-only and a new write-only output hash table becomes available. What is important is that only the method of communication changes — the amount of communication and available space per machine is constrained exactly in the same way as in the MPC model. Hence, at a high level the added capability of the AMPC model is that each machine can choose what data to read, instead of being provided a piece of data.

Computation in the AMPC model. Once all machines have completed a round of computation, the data they produced is saved to a distributed hash table. In the following round, each machine can read arbitrary values from this distributed hash table and write to a new distributed hash table.

Algorithms and Empirical Evaluation
This seemingly small difference in the way machines communicate allowed us to design much faster algorithms to a number of basic graph problems. In particular, we show that it is possible to find connected components, minimum spanning tree, maximal matching and maximal independent set in a constant number of rounds, regardless of the size of the graph.

To investigate the practical applicability of the AMPC algorithms, we have instantiated the model by combining Flume C++ (a C++ counterpart of FlumeJava) with a DHT communication layer. We have evaluated our AMPC algorithms for minimum spanning tree, maximal independent set and maximum matching and observed that we can achieve up to 7x speedups over implementations that did not use a DHT. At the same time, the AMPC implementations used 10x fewer rounds on average to complete, and also wrote less data to disk.

Our implementation of the AMPC model took advantage of hardware-accelerated remote direct memory access (RDMA), a technology that allows reading from the memory of a remote machine with a latency of a few microseconds, which is just an order of magnitude slower than reading from local memory. While some of the AMPC algorithms communicated more data than their MPC counterparts, they were overall faster, as they performed mostly fast reads using RDMA, instead of costly writes to disk.

Conclusion
With the AMPC model, we built a theoretical framework inspired by practically efficient implementations, and then developed new theoretical algorithms that delivered good empirical performance and maintained good fault-tolerance properties. We’ve been happy to see that the AMPC model has already been the subject of further study and are excited to learn what other problems can be solved more efficiently using the AMPC model or its practical implementations.

Acknowledgements
Co-authors on the two papers covered in this blog post include Soheil Behnezhad, Laxman Dhulipala, Hossein Esfandiari, and Warren Schudy. We also thank members of the Graph Mining team for their collaborations, and especially Mohammad Hossein Bateni for his input on this post. To learn more about our recent work on scalable graph algorithms, see videos from our recent Graph Mining and Learning workshop.

Today, we continue our exploration of multi-step time-series forecasting with torch. This post is the third in a series.

• Initially, we covered basics of recurrent neural networks (RNNs), and trained a model to predict the very next value in a sequence. We also found we could forecast quite a few steps ahead by feeding back individual predictions in a loop.

• Next, we built a model “natively” for multi-step prediction. A small multi-layer-perceptron (MLP) was used to project RNN output to several time points in the future.

Of both approaches, the latter was the more successful. But conceptually, it has an unsatisfying touch to it: When the MLP extrapolates and generates output for, say, ten consecutive points in time, there is no causal relation between those. (Imagine a weather forecast for ten days that never got updated.)

Now, we’d like to try something more intuitively appealing. The input is a sequence; the output is a sequence. In natural language processing (NLP), this type of task is very common: It’s exactly the kind of situation we see with machine translation or summarization.

Quite fittingly, the types of models employed to these ends are named sequence-to-sequence models (often abbreviated seq2seq). In a nutshell, they split up the task into two components: an encoding and a decoding part. The former is done just once per input-target pair. The latter is done in a loop, as in our first try. But the decoder has more information at its disposal: At each iteration, its processing is based on the previous prediction as well as previous state. That previous state will be the encoder’s when a loop is started, and its own ever thereafter.

Before discussing the model in detail, we need to adapt our data input mechanism.

Data input

We continue working with vic_elec , provided by tsibbledata.

Again, the dataset definition in the current post looks a bit different from the way it did before; it’s the shape of the target that differs. This time, y equals x, shifted to the left by one.

The reason we do this is owed to the way we are going to train the network. With seq2seq, people often use a technique called “teacher forcing” where, instead of feeding back its own prediction into the decoder module, you pass it the value it should have predicted. To be clear, this is done during training only, and to a configurable degree.

n_timesteps <- 7 * 24 * 2
n_forecast <- n_timesteps

vic_elec_get_year <- function(year, month = NULL) {
  vic_elec %>%
    filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else month) %>%
    as_tibble() %>%
    select(Demand)
}

elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix()

train_mean <- mean(elec_train)
train_sd <- sd(elec_train)

elec_dataset <- dataset(
  name = "elec_dataset",
  
  initialize = function(x, n_timesteps, sample_frac = 1) {
    
    self$n_timesteps <- n_timesteps
    self$x <- torch_tensor((x - train_mean) / train_sd)
    
    n <- length(self$x) - self$n_timesteps - 1
    
    self$starts <- sort(sample.int(
      n = n,
      size = n * sample_frac
    ))
    
  },
  
  .getitem = function(i) {
    
    start <- self$starts[i]
    end <- start + self$n_timesteps - 1
    lag <- 1
    
    list(
      x = self$x[start:end],
      y = self$x[(start+lag):(end+lag)]$squeeze(2)
    )
    
  },
  
  .length = function() {
    length(self$starts) 
  }
)

Dataset as well as dataloader instantations then can proceed as before.

batch_size <- 32

train_ds <- elec_dataset(elec_train, n_timesteps, sample_frac = 0.5)
train_dl <- train_ds %>% dataloader(batch_size = batch_size, shuffle = TRUE)

valid_ds <- elec_dataset(elec_valid, n_timesteps, sample_frac = 0.5)
valid_dl <- valid_ds %>% dataloader(batch_size = batch_size)

test_ds <- elec_dataset(elec_test, n_timesteps)
test_dl <- test_ds %>% dataloader(batch_size = 1)

Model

Technically, the model consists of three modules: the aforementioned encoder and decoder, and the seq2seq module that orchestrates them.

Encoder

The encoder takes its input and runs it through an RNN. Of the two things returned by a recurrent neural network, outputs and state, so far we’ve only been using output. This time, we do the opposite: We throw away the outputs, and only return the state.

If the RNN in question is a GRU (and assuming that of the outputs, we take just the final time step, which is what we’ve been doing throughout), there really is no difference: The final state equals the final output. If it’s an LSTM, however, there is a second kind of state, the “cell state”. In that case, returning the state instead of the final output will carry more information.

encoder_module <- nn_module(
  
  initialize = function(type, input_size, hidden_size, num_layers = 1, dropout = 0) {
    
    self$type <- type
    
    self$rnn <- if (self$type == "gru") {
      nn_gru(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        dropout = dropout,
        batch_first = TRUE
      )
    } else {
      nn_lstm(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        dropout = dropout,
        batch_first = TRUE
      )
    }
    
  },
  
  forward = function(x) {
    
    x <- self$rnn(x)
    
    # return last states for all layers
    # per layer, a single tensor for GRU, a list of 2 tensors for LSTM
    x <- x[[2]]
    x
    
  }
  
)

Decoder

In the decoder, just like in the encoder, the main component is an RNN. In contrast to previously-shown architectures, though, it does not just return a prediction. It also reports back the RNN’s final state.

decoder_module <- nn_module(
  
  initialize = function(type, input_size, hidden_size, num_layers = 1) {
    
    self$type <- type
    
    self$rnn <- if (self$type == "gru") {
      nn_gru(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        batch_first = TRUE
      )
    } else {
      nn_lstm(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        batch_first = TRUE
      )
    }
    
    self$linear <- nn_linear(hidden_size, 1)
    
  },
  
  forward = function(x, state) {
    
    # input to forward:
    # x is (batch_size, 1, 1)
    # state is (1, batch_size, hidden_size)
    x <- self$rnn(x, state)
    
    # break up RNN return values
    # output is (batch_size, 1, hidden_size)
    # next_hidden is
    c(output, next_hidden) %<-% x
    
    output <- output$squeeze(2)
    output <- self$linear(output)
    
    list(output, next_hidden)
    
  }
  
)

seq2seq module

seq2seq is where the action happens. The plan is to encode once, then call the decoder in a loop.

If you look back to decoder forward(), you see that it takes two arguments: x and state.

Depending on the context, x corresponds to one of three things: final input, preceding prediction, or prior ground truth.

• The very first time the decoder is called on an input sequence, x maps to the final input value. This is different from a task like machine translation, where you would pass in a start token. With time series, though, we’d like to continue where the actual measurements stop.

• In further calls, we want the decoder to continue from its most recent prediction. It is only logical, thus, to pass back the preceding forecast.

• That said, in NLP a technique called “teacher forcing” is commonly used to speed up training. With teacher forcing, instead of the forecast we pass the actual ground truth, the thing the decoder should have predicted. We do that only in a configurable fraction of cases, and – naturally – only while training. The rationale behind this technique is that without this form of re-calibration, consecutive prediction errors can quickly erase any remaining signal.

state, too, is polyvalent. But here, there are just two possibilities: encoder state and decoder state.

• The first time the decoder is called, it is “seeded” with the final state from the encoder. Note how this is the only time we make use of the encoding.

• From then on, the decoder’s own previous state will be passed. Remember how it returns two values, forecast and state?

seq2seq_module <- nn_module(
  
  initialize = function(type, input_size, hidden_size, n_forecast, num_layers = 1, encoder_dropout = 0) {
    
    self$encoder <- encoder_module(type = type, input_size = input_size,
                                   hidden_size = hidden_size, num_layers, encoder_dropout)
    self$decoder <- decoder_module(type = type, input_size = input_size,
                                   hidden_size = hidden_size, num_layers)
    self$n_forecast <- n_forecast
    
  },
  
  forward = function(x, y, teacher_forcing_ratio) {
    
    # prepare empty output
    outputs <- torch_zeros(dim(x)[1], self$n_forecast)$to(device = device)
    
    # encode current input sequence
    hidden <- self$encoder(x)
    
    # prime decoder with final input value and hidden state from the encoder
    out <- self$decoder(x[ , n_timesteps, , drop = FALSE], hidden)
    
    # decompose into predictions and decoder state
    # pred is (batch_size, 1)
    # state is (1, batch_size, hidden_size)
    c(pred, state) %<-% out
    
    # store first prediction
    outputs[ , 1] <- pred$squeeze(2)
    
    # iterate to generate remaining forecasts
    for (t in 2:self$n_forecast) {
      
      # call decoder on either ground truth or previous prediction, plus previous decoder state
      teacher_forcing <- runif(1) < teacher_forcing_ratio
      input <- if (teacher_forcing == TRUE) y[ , t - 1, drop = FALSE] else pred
      input <- input$unsqueeze(3)
      out <- self$decoder(input, state)
      
      # again, decompose decoder return values
      c(pred, state) %<-% out
      # and store current prediction
      outputs[ , t] <- pred$squeeze(2)
    }
    outputs
  }
  
)

net <- seq2seq_module("gru", input_size = 1, hidden_size = 32, n_forecast = n_forecast)

# training RNNs on the GPU currently prints a warning that may clutter 
# the console
# see https://github.com/mlverse/torch/issues/461
# alternatively, use 
# device <- "cpu"
device <- torch_device(if (cuda_is_available()) "cuda" else "cpu")

net <- net$to(device = device)

Training

The training procedure is mainly unchanged. We do, however, need to decide about teacher_forcing_ratio, the proportion of input sequences we want to perform re-calibration on. In valid_batch(), this should always be 0, while in train_batch(), it’s up to us (or rather, experimentation). Here, we set it to 0.3.

optimizer <- optim_adam(net$parameters, lr = 0.001)

num_epochs <- 50

train_batch <- function(b, teacher_forcing_ratio) {
  
  optimizer$zero_grad()
  output <- net(b$x$to(device = device), b$y$to(device = device), teacher_forcing_ratio)
  target <- b$y$to(device = device)
  
  loss <- nnf_mse_loss(output, target)
  loss$backward()
  optimizer$step()
  
  loss$item()
  
}

valid_batch <- function(b, teacher_forcing_ratio = 0) {
  
  output <- net(b$x$to(device = device), b$y$to(device = device), teacher_forcing_ratio)
  target <- b$y$to(device = device)
  
  loss <- nnf_mse_loss(output, target)
  
  loss$item()
  
}

for (epoch in 1:num_epochs) {
  
  net$train()
  train_loss <- c()
  
  coro::loop(for (b in train_dl) {
    loss <-train_batch(b, teacher_forcing_ratio = 0.3)
    train_loss <- c(train_loss, loss)
  })
  
  cat(sprintf("nEpoch %d, training: loss: %3.5f n", epoch, mean(train_loss)))
  
  net$eval()
  valid_loss <- c()
  
  coro::loop(for (b in valid_dl) {
    loss <- valid_batch(b)
    valid_loss <- c(valid_loss, loss)
  })
  
  cat(sprintf("nEpoch %d, validation: loss: %3.5f n", epoch, mean(valid_loss)))
}

Epoch 1, training: loss: 0.37961 

Epoch 1, validation: loss: 1.10699 

Epoch 2, training: loss: 0.19355 

Epoch 2, validation: loss: 1.26462 

# ...
# ...

Epoch 49, training: loss: 0.03233 

Epoch 49, validation: loss: 0.62286 

Epoch 50, training: loss: 0.03091 

Epoch 50, validation: loss: 0.54457

It’s interesting to compare performances for different settings of teacher_forcing_ratio. With a setting of 0.5, training loss decreases a lot more slowly; the opposite is seen with a setting of 0. Validation loss, however, is not affected significantly.

Evaluation

The code to inspect test-set forecasts is unchanged.

net$eval()

test_preds <- vector(mode = "list", length = length(test_dl))

i <- 1

coro::loop(for (b in test_dl) {
  
  input <- b$x
  output <- net(input$to(device = device))
  preds <- as.numeric(output)
  
  test_preds[[i]] <- preds
  i <<- i + 1
  
})

vic_elec_jan_2014 <- vic_elec %>%
  filter(year(Date) == 2014, month(Date) == 1)

test_pred1 <- test_preds[[1]]
test_pred1 <- c(rep(NA, n_timesteps), test_pred1, rep(NA, nrow(vic_elec_jan_2014) - n_timesteps - n_forecast))

test_pred2 <- test_preds[[408]]
test_pred2 <- c(rep(NA, n_timesteps + 407), test_pred2, rep(NA, nrow(vic_elec_jan_2014) - 407 - n_timesteps - n_forecast))

test_pred3 <- test_preds[[817]]
test_pred3 <- c(rep(NA, nrow(vic_elec_jan_2014) - n_forecast), test_pred3)


preds_ts <- vic_elec_jan_2014 %>%
  select(Demand) %>%
  add_column(
    mlp_ex_1 = test_pred1 * train_sd + train_mean,
    mlp_ex_2 = test_pred2 * train_sd + train_mean,
    mlp_ex_3 = test_pred3 * train_sd + train_mean) %>%
  pivot_longer(-Time) %>%
  update_tsibble(key = name)


preds_ts %>%
  autoplot() +
  scale_colour_manual(values = c("#08c5d1", "#00353f", "#ffbf66", "#d46f4d")) +
  theme_minimal()

(#fig:unnamed-chunk-8)One-week-ahead predictions for January, 2014.

Comparing this to the forecast obtained from last time’s RNN-MLP combo, we don’t see much of a difference. Is this surprising? To me it is. If asked to speculate about the reason, I would probably say this: In all of the architectures we’ve used so far, the main carrier of information has been the final hidden state of the RNN (one and only RNN in the two previous setups, encoder RNN in this one). It will be interesting to see what happens in the last part of this series, when we augment the encoder-decoder architecture by attention.

Thanks for reading!

Photo by Suzuha Kozuki on Unsplash

Posted by Michael Dixon, Software Engineer and Reena Singhal Lee, Product Manager, Google Health

People often turn to technology to manage their health and wellbeing, whether it is to record their daily exercise, measure their heart rate, or increasingly, to understand their sleep patterns. Sleep is foundational to a person’s everyday wellbeing and can be impacted by (and in turn, have an impact on) other aspects of one’s life — mood, energy, diet, productivity, and more.

As part of our ongoing efforts to support people’s health and happiness, today we announced Sleep Sensing in the new Nest Hub, which uses radar-based sleep tracking in addition to an algorithm for cough and snore detection. While not intended for medical purposes¹, Sleep Sensing is an opt-in feature that can help users better understand their nighttime wellness using a contactless bedside setup. Here we describe the technologies behind Sleep Sensing and discuss how we leverage on-device signal processing to enable sleep monitoring (comparable to other clinical- and consumer-grade devices) in a way that protects user privacy.

Soli for Sleep Tracking
Sleep Sensing in Nest Hub demonstrates the first wellness application of Soli, a miniature radar sensor that can be used for gesture sensing at various scales, from a finger tap to movements of a person’s body. In Pixel 4, Soli powers Motion Sense, enabling touchless interactions with the phone to skip songs, snooze alarms, and silence phone calls. We extended this technology and developed an embedded Soli-based algorithm that could be implemented in Nest Hub for sleep tracking.

Soli consists of a millimeter-wave frequency-modulated continuous wave (FMCW) radar transceiver that emits an ultra-low power radio wave and measures the reflected signal from the scene of interest. The frequency spectrum of the reflected signal contains an aggregate representation of the distance and velocity of objects within the scene. This signal can be processed to isolate a specified range of interest, such as a user’s sleeping area, and to detect and characterize a wide range of motions within this region, ranging from large body movements to sub-centimeter respiration.

Soli spectrogram illustrating its ability to detect a wide range of motions, characterized as (a) an empty room (no variation in the reflected signal demonstrated by the black space), (b) large pose changes, (c) brief limb movements, and (d) sub-centimeter chest and torso displacements from respiration while at rest.

In order to make use of this signal for Sleep Sensing, it was necessary to design an algorithm that could determine whether a person is present in the specified sleeping area and, if so, whether the person is asleep or awake. We designed a custom machine-learning (ML) model to efficiently process a continuous stream of 3D radar tensors (summarizing activity over a range of distances, frequencies, and time) and automatically classify each feature into one of three possible states: absent, awake, and asleep.

To train and evaluate the model, we recorded more than a million hours of radar data from thousands of individuals, along with thousands of sleep diaries, reference sensor recordings, and external annotations. We then leveraged the TensorFlow Extended framework to construct a training pipeline to process this data and produce an efficient TensorFlow Lite embedded model. In addition, we created an automatic calibration algorithm that runs during setup to configure the part of the scene on which the classifier will focus. This ensures that the algorithm ignores motion from a person on the other side of the bed or from other areas of the room, such as ceiling fans and swaying curtains.

The custom ML model efficiently processes a continuous stream of 3D radar tensors (summarizing activity over a range of distances, frequencies, and time) to automatically compute probabilities for the likelihood of user presence and wakefulness (awake or asleep).

To validate the accuracy of the algorithm, we compared it to the gold-standard of sleep-wake determination, the polysomnogram sleep study, in a cohort of 33 “healthy sleepers” (those without significant sleep issues, like sleep apnea or insomnia) across a broad age range (19-78 years of age). Sleep studies are typically conducted in clinical and research laboratories in order to collect various body signals (brain waves, muscle activity, respiratory and heart rate measurements, body movement and position, and snoring), which can then be interpreted by trained sleep experts to determine stages of sleep and identify relevant events. To account for variability in how different scorers apply the American Academy of Sleep Medicine’s staging and scoring rules, our study used two board-certified sleep technologists to independently annotate each night of sleep and establish a definitive groundtruth.

We compared our Sleep Sensing algorithm’s outputs to the corresponding groundtruth sleep and wake labels for every 30-second epoch of time to compute standard performance metrics (e.g., sensitivity and specificity). While not a true head-to-head comparison, this study’s results can be compared against previously published studies in similar cohorts with comparable methodologies in order to get a rough estimate of performance. In “Sleep-wake detection with a contactless, bedside radar sleep sensing system”, we share the full details of these validation results, demonstrating sleep-wake estimation equivalent to or, in some cases, better than current clinical and consumer sleep tracking devices.

Aggregate performance from previously published accuracies for detection of sleep (sensitivity) and wake (specificity) of a variety of sleep trackers against polysomnography in a variety of different studies, accounting for 3,990 nights in total. While this is not a head-to-head comparison, the performance of Sleep Sensing on Nest Hub in a population of healthy sleepers who simultaneously underwent polysomnography is added to the figure for rough comparison. The size of each circle is a reflection of the number of nights and the inset illustrates the mean±standard deviation for the performance metrics.

Understanding Sleep Quality with Audio Sensing
The Soli-based sleep tracking algorithm described above gives users a convenient and reliable way to see how much sleep they are getting and when sleep disruptions occur. However, to understand and improve their sleep, users also need to understand why their sleep is disrupted. To assist with this, Nest Hub uses its array of sensors to track common sleep disturbances, such as light level changes or uncomfortable room temperature. In addition to these, respiratory events like coughing and snoring are also frequent sources of disturbance, but people are often unaware of these events.

As with other audio-processing applications like speech or music recognition, coughing and snoring exhibit distinctive temporal patterns in the audio frequency spectrum, and with sufficient data an ML model can be trained to reliably recognize these patterns while simultaneously ignoring a wide variety of background noises, from a humming fan to passing cars. The model uses entirely on-device audio processing with privacy-preserving analysis, with no raw audio data sent to Google’s servers. A user can then opt to save the outputs of the processing (sound occurrences, such as the number of coughs and snore minutes) in Google Fit, in order to view personal insights and summaries of their night time wellness over time.

The Nest Hub displays when snoring and coughing may have disturbed a user’s sleep (top) and can track weekly trends (bottom).

To train the model, we assembled a large, hand-labeled dataset, drawing examples from the publicly available AudioSet research dataset as well as hundreds of thousands of additional real-world audio clips contributed by thousands of individuals.

Log-Mel spectrogram inputs comparing cough (left) and snore (right) audio snippets.

When a user opts in to cough and snore tracking on their bedside Nest Hub, the device first uses its Soli-based sleep algorithms to detect when a user goes to bed. Once it detects that a user has fallen asleep, it then activates its on-device sound sensing model and begins processing audio. The model works by continuously extracting spectrogram-like features from the audio input and feeding them through a convolutional neural network classifier in order to estimate the probability that coughing or snoring is happening at a given instant in time. These estimates are analyzed over the course of the night to produce a report of the overall cough count and snoring duration and highlight exactly when these events occurred.

Conclusion
The new Nest Hub, with its underlying Sleep Sensing features, is a first step in empowering users to understand their nighttime wellness using privacy-preserving radar and audio signals. We continue to research additional ways that ambient sensing and the predictive ability of consumer devices could help people better understand their daily health and wellness in a privacy-preserving way.

Acknowledgements
This work involved collaborative efforts from a multidisciplinary team of software engineers, researchers, clinicians, and cross-functional contributors. Special thanks to D. Shin for his significant contributions to this technology and blogpost, and Dr. Logan Schneider, visiting sleep neurologist affiliated with the Stanford/VA Alzheimer’s Center and Stanford Sleep Center, whose clinical expertise and contributions were invaluable to continuously guide this research. In addition to the authors, key contributors to this research from Google Health include Jeffrey Yu, Allen Jiang, Arno Charton, Jake Garrison, Navreet Gill, Sinan Hersek, Yijie Hong, Jonathan Hsu, Andi Janti, Ajay Kannan, Mukil Kesavan, Linda Lei, Kunal Okhandiar‎, Xiaojun Ping, Jo Schaeffer, Neil Smith, Siddhant Swaroop, Bhavana Koka, Anupam Pathak, Dr. Jim Taylor, and the extended team. Another special thanks to Ken Mixter for his support and contributions to the development and integration of this technology into Nest Hub. Thanks to Mark Malhotra and Shwetak Patel for their ongoing leadership, as well as the Nest, Fit, Soli, and Assistant teams we collaborated with to build and validate Sleep Sensing on Nest Hub.

¹ Not intended to diagnose, cure, mitigate, prevent or treat any disease or condition. ^↩

Posted by Neil Zeghidour, Research Scientist, Google Research

Developing machine learning (ML) models for audio understanding has seen tremendous progress over the past several years. Leveraging the ability to learn parameters from data, the field has progressively shifted from composite, handcrafted systems to today’s deep neural classifiers that are used to recognize speech, understand music, or classify animal vocalizations such as bird calls. However, unlike computer vision models, which can learn from raw pixels, deep neural networks for audio classification are rarely trained from raw audio waveforms. Instead, they rely on pre-processed data in the form of mel filterbanks — handcrafted mel-scaled spectrograms that have been designed to replicate some aspects of the human auditory response.

Although modeling mel filterbanks for ML tasks has been historically successful, it is limited by the inherent biases of fixed features: even though using a fixed mel-scale and a logarithmic compression works well in general, we have no guarantee that they provide the best representations for the task at hand. In particular, even though matching human perception provides good inductive biases for some application domains, e.g., speech recognition or music understanding, these biases may be detrimental to domains for which imitating the human ear is not important, such as recognizing whale calls. So, in order to achieve optimal performance, the mel filterbanks should be tailored to the task of interest, a tedious process that requires an iterative effort informed by expert domain knowledge. As a consequence, standard mel filterbanks are used for most audio classification tasks in practice, even though they are suboptimal. In addition, while researchers have proposed ML systems to address these problems, such as Time-Domain Filterbanks, SincNet and Wavegram, they have yet to match the performance of traditional mel filterbanks.

In “LEAF, A Fully Learnable Frontend for Audio Classification”, accepted at ICLR 2021, we present an alternative method for crafting learnable spectrograms for audio understanding tasks. LEarnable Audio Frontend (LEAF) is a neural network that can be initialized to approximate mel filterbanks, and then be trained jointly with any audio classifier to adapt to the task at hand, while only adding a handful of parameters to the full model. We show that over a wide range of audio signals and classification tasks, including speech, music and bird songs, LEAF spectrograms improve classification performance over fixed mel filterbanks and over previously proposed learnable systems. We have implemented the code in TensorFlow 2 and released it to the community through our GitHub repository.

Mel Filterbanks: Mimicking Human Perception of Sound
The first step in the traditional approach to creating a mel filterbank is to capture the sound’s time-variability by windowing, i.e., cutting the signal into short segments with fixed duration. Then, one performs filtering, by passing the windowed segments through a bank of fixed frequency filters, that replicate the human logarithmic sensitivity to pitch. Because we are more sensitive to variations in low frequencies than high frequencies, mel filterbanks give more importance to the low-frequency range of sounds. Finally, the audio signal is compressed to mimic the ear’s logarithmic sensitivity to loudness — a sound needs to double its power for a person to perceive an increase of 3 decibels.

LEAF loosely follows this traditional approach to mel filterbank generation, but replaces each of the fixed operations (i.e., the filtering layer, windowing layer, and compression function) by a learned counterpart. The output of LEAF is a time-frequency representation (a spectrogram) similar to mel filterbanks, but fully learnable. So, for example, while a mel filterbank uses a fixed scale for pitch, LEAF learns the scale that is best suited to the task of interest. Any model that can be trained using mel filterbanks as input features, can also be trained on LEAF spectrograms.

Diagram of computation of mel filterbanks compared to LEAF spectrograms.

While LEAF can be initialized randomly, it can also be initialized in a way that approximates mel filterbanks, which have been shown to be a better starting point. Then, LEAF can be trained with any classifier to adapt to the task of interest.

Left: Mel filterbanks for a person saying “wow”. Right: LEAF’s output for the same example, after training on a dataset of speech commands.

A Parameter-Efficient Alternative to Fixed Features
A potential downside of replacing fixed features that involve no learnable parameter with a trainable system is that it can significantly increase the number of parameters to optimize. To avoid this issue, LEAF uses Gabor convolution layers that have only two parameters per filter, instead of the ~400 parameters typical of a standard convolution layer. This way, even when paired with a small classifier, such as EfficientNetB0, the LEAF model only accounts for 0.01% of the total parameters.

Top: Unconstrained convolutional filters after training for audio event classification. Bottom: LEAF filters at convergence after training for the same task.

Performance
We apply LEAF to diverse audio classification tasks, including recognizing speech commands, speaker identification, acoustic scene recognition, identifying musical instruments, and finding birdsongs. On average, LEAF outperforms both mel filterbanks and previous learnable frontends, such as Time-Domain Filterbanks, SincNet and Wavegram. In particular, LEAF achieves a 76.9% average accuracy across the different tasks, compared to 73.9% for mel filterbanks. Moreover we show that LEAF can be trained in a multi-task setting, such that a single LEAF parametrization can work well across all these tasks. Finally, when combined with a large audio classifier, LEAF reaches state-of-the-art performance on the challenging AudioSet benchmark, with a 2.74 d-prime score.

D-prime score (the higher the better) of LEAF, mel filterbanks and previously proposed learnable spectrograms on the evaluation set of AudioSet.

Conclusion
The scope of audio understanding tasks keeps growing, from diagnosing dementia from speech to detecting humpback whale calls from underwater microphones. Adapting mel filterbanks to every new task can require a significant amount of hand-tuning and experimentation. In this context, LEAF provides a drop-in replacement for these fixed features, that can be trained to adapt to the task of interest, with minimal task-specific adjustments. Thus, we believe that LEAF can accelerate development of models for new audio understanding tasks.

Acknowledgements
We thank our co-authors, Olivier Teboul, Félix de Chaumont-Quitry and Marco Tagliasacchi. We also thank Dick Lyon, Vincent Lostanlen, Matt Harvey, and Alex Park for helpful discussions, and Julie Thomas for helping to design figures for this post.

We pick up where the first post in this series left us: confronting the task of multi-step time-series forecasting.

Our first attempt was a workaround of sorts. The model had been trained to deliver a single prediction, corresponding to the very next point in time. Thus, if we needed a longer forecast, all we could do is use that prediction and feed it back to the model, moving the input sequence by one value (from ([x_{t-n}, …, x_t]) to ([x_{t-n-1}, …, x_{t+1}]), say).

In contrast, the new model will be designed – and trained – to forecast a configurable number of observations at once. The architecture will still be basic – about as basic as possible, given the task – and thus, can serve as a baseline for later attempts.

Data input

We work with the same data as before, vic_elec from tsibbledata.

Compared to last time though, the dataset class has to change. While, previously, for each batch item the target (y) was a single value, it now is a vector, just like the input, x. And just like n_timesteps was (and still is) used to specify the length of the input sequence, there is now a second parameter, n_forecast, to configure target size.

In our example, n_timesteps and n_forecast are set to the same value, but there is no need for this to be the case. You could equally well train on week-long sequences and then forecast developments over a single day, or a month.

Apart from the fact that .getitem() now returns a vector for y as well as x, there is not much to be said about dataset creation. Here is the complete code to set up the data input pipeline:

n_timesteps <- 7 * 24 * 2
n_forecast <- 7 * 24 * 2 
batch_size <- 32

vic_elec_get_year <- function(year, month = NULL) {
  vic_elec %>%
    filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else month) %>%
    as_tibble() %>%
    select(Demand)
}

elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix()

train_mean <- mean(elec_train)
train_sd <- sd(elec_train)

elec_dataset <- dataset(
  name = "elec_dataset",
  
  initialize = function(x, n_timesteps, n_forecast, sample_frac = 1) {
    
    self$n_timesteps <- n_timesteps
    self$n_forecast <- n_forecast
    self$x <- torch_tensor((x - train_mean) / train_sd)
    
    n <- length(self$x) - self$n_timesteps - self$n_forecast + 1
    
    self$starts <- sort(sample.int(
      n = n,
      size = n * sample_frac
    ))
    
  },
  
  .getitem = function(i) {
    
    start <- self$starts[i]
    end <- start + self$n_timesteps - 1
    pred_length <- self$n_forecast
    
    list(
      x = self$x[start:end],
      y = self$x[(end + 1):(end + pred_length)]$squeeze(2)
    )
    
  },
  
  .length = function() {
    length(self$starts) 
  }
)

train_ds <- elec_dataset(elec_train, n_timesteps, n_forecast, sample_frac = 0.5)
train_dl <- train_ds %>% dataloader(batch_size = batch_size, shuffle = TRUE)

valid_ds <- elec_dataset(elec_valid, n_timesteps, n_forecast, sample_frac = 0.5)
valid_dl <- valid_ds %>% dataloader(batch_size = batch_size)

test_ds <- elec_dataset(elec_test, n_timesteps, n_forecast)
test_dl <- test_ds %>% dataloader(batch_size = 1)

Model

The model replaces the single linear layer that, in the previous post, had been tasked with outputting the final prediction, with a small network, complete with two linear layers and – optional – dropout.

In forward(), we first apply the RNN, and just like in the previous post, we make use of the outputs only; or more specifically, the output corresponding to the final time step. (See that previous post for a detailed discussion of what a torch RNN returns.)

model <- nn_module(
  
  initialize = function(type, input_size, hidden_size, linear_size, output_size,
                        num_layers = 1, dropout = 0, linear_dropout = 0) {
    
    self$type <- type
    self$num_layers <- num_layers
    self$linear_dropout <- linear_dropout
    
    self$rnn <- if (self$type == "gru") {
      nn_gru(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        dropout = dropout,
        batch_first = TRUE
      )
    } else {
      nn_lstm(
        input_size = input_size,
        hidden_size = hidden_size,
        num_layers = num_layers,
        dropout = dropout,
        batch_first = TRUE
      )
    }
    
    self$mlp <- nn_sequential(
      nn_linear(hidden_size, linear_size),
      nn_relu(),
      nn_dropout(linear_dropout),
      nn_linear(linear_size, output_size)
    )
    
  },
  
  forward = function(x) {
    
    x <- self$rnn(x)
    x[[1]][ ,-1, ..] %>% 
      self$mlp()
    
  }
  
)

For model instantiation, we now have an additional configuration parameter, related to the amount of dropout between the two linear layers.

net <- model(
  "gru", input_size = 1, hidden_size = 32, linear_size = 512, output_size = n_forecast, linear_dropout = 0
  )

# training RNNs on the GPU currently prints a warning that may clutter 
# the console
# see https://github.com/mlverse/torch/issues/461
# alternatively, use 
# device <- "cpu"
device <- torch_device(if (cuda_is_available()) "cuda" else "cpu")

net <- net$to(device = device)

Training

The training procedure is completely unchanged.

optimizer <- optim_adam(net$parameters, lr = 0.001)

num_epochs <- 30

train_batch <- function(b) {
  
  optimizer$zero_grad()
  output <- net(b$x$to(device = device))
  target <- b$y$to(device = device)
  
  loss <- nnf_mse_loss(output, target)
  loss$backward()
  optimizer$step()
  
  loss$item()
}

valid_batch <- function(b) {
  
  output <- net(b$x$to(device = device))
  target <- b$y$to(device = device)
  
  loss <- nnf_mse_loss(output, target)
  loss$item()
  
}

for (epoch in 1:num_epochs) {
  
  net$train()
  train_loss <- c()
  
  coro::loop(for (b in train_dl) {
    loss <-train_batch(b)
    train_loss <- c(train_loss, loss)
  })
  
  cat(sprintf("nEpoch %d, training: loss: %3.5f n", epoch, mean(train_loss)))
  
  net$eval()
  valid_loss <- c()
  
  coro::loop(for (b in valid_dl) {
    loss <- valid_batch(b)
    valid_loss <- c(valid_loss, loss)
  })
  
  cat(sprintf("nEpoch %d, validation: loss: %3.5f n", epoch, mean(valid_loss)))
}

# Epoch 1, training: loss: 0.65737 
# 
# Epoch 1, validation: loss: 0.54586 
# 
# Epoch 2, training: loss: 0.43991 
# 
# Epoch 2, validation: loss: 0.50588 
# 
# Epoch 3, training: loss: 0.42161 
# 
# Epoch 3, validation: loss: 0.50031 
# 
# Epoch 4, training: loss: 0.41718 
# 
# Epoch 4, validation: loss: 0.48703 
# 
# Epoch 5, training: loss: 0.39498 
# 
# Epoch 5, validation: loss: 0.49572 
# 
# Epoch 6, training: loss: 0.38073 
# 
# Epoch 6, validation: loss: 0.46813 
# 
# Epoch 7, training: loss: 0.36472 
# 
# Epoch 7, validation: loss: 0.44957 
# 
# Epoch 8, training: loss: 0.35058 
# 
# Epoch 8, validation: loss: 0.44440 
# 
# Epoch 9, training: loss: 0.33880 
# 
# Epoch 9, validation: loss: 0.41995 
# 
# Epoch 10, training: loss: 0.32545 
# 
# Epoch 10, validation: loss: 0.42021 
# 
# Epoch 11, training: loss: 0.31347 
# 
# Epoch 11, validation: loss: 0.39514 
# 
# Epoch 12, training: loss: 0.29622 
# 
# Epoch 12, validation: loss: 0.38146 
# 
# Epoch 13, training: loss: 0.28006 
# 
# Epoch 13, validation: loss: 0.37754 
# 
# Epoch 14, training: loss: 0.27001 
# 
# Epoch 14, validation: loss: 0.36636 
# 
# Epoch 15, training: loss: 0.26191 
# 
# Epoch 15, validation: loss: 0.35338 
# 
# Epoch 16, training: loss: 0.25533 
# 
# Epoch 16, validation: loss: 0.35453 
# 
# Epoch 17, training: loss: 0.25085 
# 
# Epoch 17, validation: loss: 0.34521 
# 
# Epoch 18, training: loss: 0.24686 
# 
# Epoch 18, validation: loss: 0.35094 
# 
# Epoch 19, training: loss: 0.24159 
# 
# Epoch 19, validation: loss: 0.33776 
# 
# Epoch 20, training: loss: 0.23680 
# 
# Epoch 20, validation: loss: 0.33974 
# 
# Epoch 21, training: loss: 0.23070 
# 
# Epoch 21, validation: loss: 0.34069 
# 
# Epoch 22, training: loss: 0.22761 
# 
# Epoch 22, validation: loss: 0.33724 
# 
# Epoch 23, training: loss: 0.22390 
# 
# Epoch 23, validation: loss: 0.34013 
# 
# Epoch 24, training: loss: 0.22155 
# 
# Epoch 24, validation: loss: 0.33460 
# 
# Epoch 25, training: loss: 0.21820 
# 
# Epoch 25, validation: loss: 0.33755 
# 
# Epoch 26, training: loss: 0.22134 
# 
# Epoch 26, validation: loss: 0.33678 
# 
# Epoch 27, training: loss: 0.21061 
# 
# Epoch 27, validation: loss: 0.33108 
# 
# Epoch 28, training: loss: 0.20496 
# 
# Epoch 28, validation: loss: 0.32769 
# 
# Epoch 29, training: loss: 0.20223 
# 
# Epoch 29, validation: loss: 0.32969 
# 
# Epoch 30, training: loss: 0.20022 
# 
# Epoch 30, validation: loss: 0.33331 

From the way loss decreases on the training set, we conclude that, yes, the model is learning something. It probably would continue improving for quite some epochs still. We do, however, see less of an improvement on the validation set.

Naturally, now we’re curious about test-set predictions. (Remember, for testing we’re choosing the “particularly hard” month of January, 2014 – particularly hard because of a heatwave that resulted in exceptionally high demand.)

Evaluation

With no loop to be coded, evaluation now becomes pretty straightforward:

net$eval()

test_preds <- vector(mode = "list", length = length(test_dl))

i <- 1

coro::loop(for (b in test_dl) {
  
  input <- b$x
  output <- net(input$to(device = device))
  preds <- as.numeric(output)
  
  test_preds[[i]] <- preds
  i <<- i + 1
  
})

vic_elec_jan_2014 <- vic_elec %>%
  filter(year(Date) == 2014, month(Date) == 1)

test_pred1 <- test_preds[[1]]
test_pred1 <- c(rep(NA, n_timesteps), test_pred1, rep(NA, nrow(vic_elec_jan_2014) - n_timesteps - n_forecast))

test_pred2 <- test_preds[[408]]
test_pred2 <- c(rep(NA, n_timesteps + 407), test_pred2, rep(NA, nrow(vic_elec_jan_2014) - 407 - n_timesteps - n_forecast))

test_pred3 <- test_preds[[817]]
test_pred3 <- c(rep(NA, nrow(vic_elec_jan_2014) - n_forecast), test_pred3)


preds_ts <- vic_elec_jan_2014 %>%
  select(Demand) %>%
  add_column(
    mlp_ex_1 = test_pred1 * train_sd + train_mean,
    mlp_ex_2 = test_pred2 * train_sd + train_mean,
    mlp_ex_3 = test_pred3 * train_sd + train_mean) %>%
  pivot_longer(-Time) %>%
  update_tsibble(key = name)


preds_ts %>%
  autoplot() +
  scale_colour_manual(values = c("#08c5d1", "#00353f", "#ffbf66", "#d46f4d")) +
  theme_minimal()

(#fig:unnamed-chunk-6)One-week-ahead predictions for January, 2014.

Compare this to the forecast obtained by feeding back predictions. The demand profiles over the day look a lot more realistic now. How about the phases of extreme demand? Evidently, these are not reflected in the forecast, not any more than in the “loop technique”. In fact, the forecast allows for interesting insights into this model’s personality: Apparently, it really likes fluctuating around the mean – “prime” it with inputs that oscillate around a significantly higher level, and it will quickly shift back to its comfort zone.

Discussion

Seeing how, above, we provided an option to use dropout inside the MLP, you may be wondering if this would help with forecasts on the test set. Turns out it did not, in my experiments. Maybe this is not so strange either: How, absent external cues (temperature), should the network know that high demand is coming up?

In our analysis, we can make an additional distinction. With the first week of predictions, what we see is a failure to anticipate something that could not reasonably have been anticipated (two, or two-and-a-half, say, days of exceptionally high demand). In the second, all the network would have had to do was stay at the current, elevated level. It will be interesting to see how this is handled by the architectures we discuss next.

Finally, an additional idea you may have had is – what if we used temperature as a second input variable? As a matter of fact, training performance indeed improved, but no performance impact was observed on the validation and test sets. Still, you may find the code useful – it is easily extended to datasets with more predictors. Therefore, we reproduce it in the appendix.

Thanks for reading!

Appendix

# Data input code modified to accommodate two predictors

n_timesteps <- 7 * 24 * 2
n_forecast <- 7 * 24 * 2

vic_elec_get_year <- function(year, month = NULL) {
  vic_elec %>%
    filter(year(Date) == year, month(Date) == if (is.null(month)) month(Date) else month) %>%
    as_tibble() %>%
    select(Demand, Temperature)
}

elec_train <- vic_elec_get_year(2012) %>% as.matrix()
elec_valid <- vic_elec_get_year(2013) %>% as.matrix()
elec_test <- vic_elec_get_year(2014, 1) %>% as.matrix()

train_mean_demand <- mean(elec_train[ , 1])
train_sd_demand <- sd(elec_train[ , 1])

train_mean_temp <- mean(elec_train[ , 2])
train_sd_temp <- sd(elec_train[ , 2])

elec_dataset <- dataset(
  name = "elec_dataset",
  
  initialize = function(data, n_timesteps, n_forecast, sample_frac = 1) {
    
    demand <- (data[ , 1] - train_mean_demand) / train_sd_demand
    temp <- (data[ , 2] - train_mean_temp) / train_sd_temp
    self$x <- cbind(demand, temp) %>% torch_tensor()
    
    self$n_timesteps <- n_timesteps
    self$n_forecast <- n_forecast
    
    n <- nrow(self$x) - self$n_timesteps - self$n_forecast + 1
    self$starts <- sort(sample.int(
      n = n,
      size = n * sample_frac
    ))
    
  },
  
  .getitem = function(i) {
    
    start <- self$starts[i]
    end <- start + self$n_timesteps - 1
    pred_length <- self$n_forecast
    
    list(
      x = self$x[start:end, ],
      y = self$x[(end + 1):(end + pred_length), 1]
    )
    
  },
  
  .length = function() {
    length(self$starts)
  }
  
)

### rest identical to single-predictor code above

Photo by Monica Bourgeau on Unsplash