As neural network models and training data size grow, training efficiency is becoming an important focus for deep learning. For example, GPT-3 demonstrates remarkable capability in few-shot learning, but it requires weeks of training with thousands of GPUs, making it difficult to retrain or improve. What if, instead, one could design neural networks that were smaller and faster, yet still more accurate?
In this post, we introduce two families of models for image recognition that leverage neural architecture search, and a principled design methodology based on model capacity and generalization. The first is EfficientNetV2 (accepted at ICML 2021), which consists of convolutional neural networks that aim for fast training speed for relatively small-scale datasets, such as ImageNet1k (with 1.28 million images). The second family is CoAtNet, which are hybrid models that combine convolution and self-attention, with the goal of achieving higher accuracy on large-scale datasets, such as ImageNet21 (with 13 million images) and JFT (with billions of images). Compared to previous results, our models are 4-10x faster while achieving new state-of-the-art 90.88% top-1 accuracy on the well-established ImageNet dataset. We are also releasing the source code and pretrained models on the Google AutoML github.
EfficientNetV2: Smaller Models and Faster Training
EfficientNetV2 is based upon the previous EfficientNet architecture. To improve upon the original, we systematically studied the training speed bottlenecks on modern TPUs/GPUs and found: (1) training with very large image sizes results in higher memory usage and thus is often slower on TPUs/GPUs; (2) the widely used depthwise convolutions are inefficient on TPUs/GPUs, because they exhibit low hardware utilization; and (3) the commonly used uniform compound scaling approach, which scales up every stage of convolutional networks equally, is sub-optimal. To address these issues, we propose both a training-aware neural architecture search (NAS), in which the training speed is included in the optimization goal, and a scaling method that scales different stages in a non-uniform manner.
The training-aware NAS is based on the previous platform-aware NAS, but unlike the original approach, which mostly focuses on inference speed, here we jointly optimize model accuracy, model size, and training speed. We also extend the original search space to include more accelerator-friendly operations, such as FusedMBConv, and simplify the search space by removing unnecessary operations, such as average pooling and max pooling, which are never selected by NAS. The resulting EfficientNetV2 networks achieve improved accuracy over all previous models, while being much faster and up to 6.8x smaller.
To further speed up the training process, we also propose an enhanced method of progressive learning, which gradually changes image size and regularization magnitude during training. Progressive training has been used in image classification, GANs, and language models. This approach focuses on image classification, but unlike previous approaches that often trade accuracy for improved training speed, can slightly improve the accuracy while also significantly reducing training time. The key idea in our improved approach is to adaptively change regularization strength, such as dropout ratio or data augmentation magnitude, according to the image size. For the same network, small image size leads to lower network capacity and thus requires weak regularization; vice versa, a large image size requires stronger regularization to combat overfitting.
 |
| Progressive learning for EfficientNetV2. Here we mainly focus on three types of regularizations: data augmentation, mixup, and dropout. |
We evaluate the EfficientNetV2 models on ImageNet and a few transfer learning datasets, such as CIFAR-10/100, Flowers, and Cars. On ImageNet, EfficientNetV2 significantly outperforms previous models with about 5–11x faster training speed and up to 6.8x smaller model size, without any drop in accuracy.
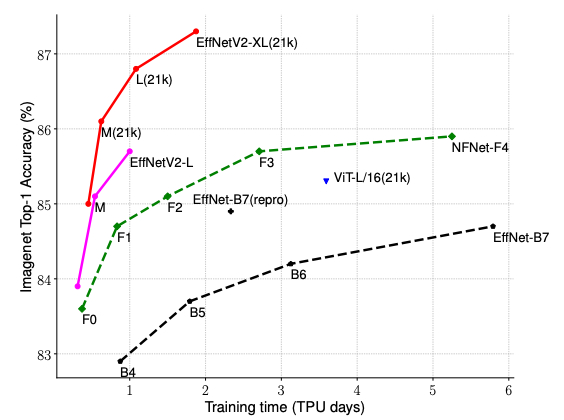 |
| EfficientNetV2 achieves much better training efficiency than prior models for ImageNet classification. |
CoAtNet: Fast and Accurate Models for Large-Scale Image Recognition
While EfficientNetV2 is still a typical convolutional neural network, recent studies on Vision Transformer (ViT) have shown that attention-based transformer models could perform better than convolutional neural networks on large-scale datasets like JFT-300M. Inspired by this observation, we further expand our study beyond convolutional neural networks with the aim of finding faster and more accurate vision models.
In “CoAtNet: Marrying Convolution and Attention for All Data Sizes”, we systematically study how to combine convolution and self-attention to develop fast and accurate neural networks for large-scale image recognition. Our work is based on an observation that convolution often has better generalization (i.e., the performance gap between training and evaluation) due to its inductive bias, while self-attention tends to have greater capacity (i.e., the ability to fit large-scale training data) thanks to its global receptive field. By combining convolution and self-attention, our hybrid models can achieve both better generalization and greater capacity.
We observe two key insights from our study: (1) depthwise convolution and self-attention can be naturally unified via simple relative attention, and (2) vertically stacking convolution layers and attention layers in a way that considers their capacity and computation required in each stage (resolution) is surprisingly effective in improving generalization, capacity and efficiency. Based on these insights, we have developed a family of hybrid models with both convolution and attention, named CoAtNets (pronounced “coat” nets). The following figure shows the overall CoAtNet network architecture:
 |
| Overall CoAtNet architecture. Given an input image with size HxW, we first apply convolutions in the first stem stage (S0) and reduce the size to H/2 x W/2. The size continues to reduce with each stage. Ln refers to the number of layers. Then, the early two stages (S1 and S2) mainly adopt MBConv building blocks consisting of depthwise convolution. The later two stages (S3 and S4) mainly adopt Transformer blocks with relative self-attention. Unlike the previous Transformer blocks in ViT, here we use pooling between stages, similar to Funnel Transformer. Finally, we apply a classification head to generate class prediction. |
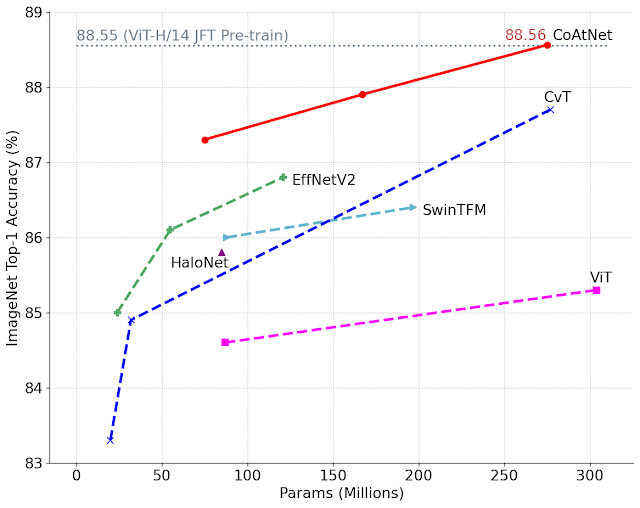
CoAtNet models consistently outperform ViT models and its variants across a number of datasets, such as ImageNet1K, ImageNet21K, and JFT. When compared to convolutional networks, CoAtNet exhibits comparable performance on a small-scale dataset (ImageNet1K) and achieves substantial gains as the data size increases (e.g. on ImageNet21K and JFT).
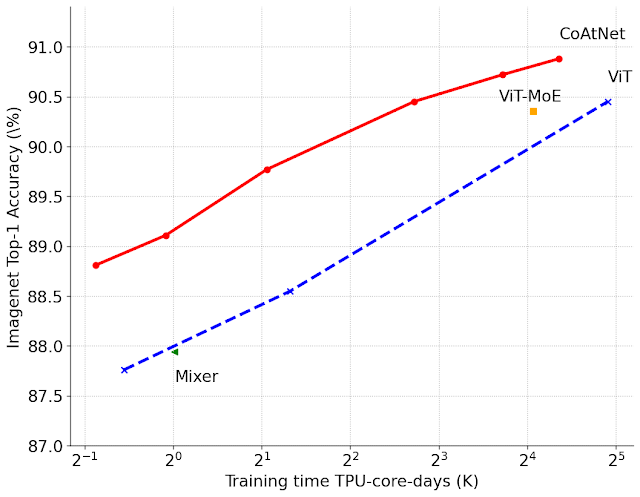
We also evaluated CoAtNets on the large-scale JFT dataset. To reach a similar accuracy target, CoAtNet trains about 4x faster than previous ViT models and more importantly, achieves a new state-of-the-art top-1 accuracy on ImageNet of 90.88%.
Conclusion and Future Work
In this post, we introduce two families of neural networks, named EfficientNetV2 and CoAtNet, which achieve state-of-the-art performance on image recognition. All EfficientNetV2 models are open sourced and the pretrained models are also available on the TFhub. CoAtNet models will also be open-sourced soon. We hope these new neural networks can benefit the research community and the industry. In the future we plan to further optimize these models and apply them to new tasks, such as zero-shot learning and self-supervised learning, which often require fast models with high capacity.
Acknowledgements
Special thanks to our co-authors Hanxiao Liu and Quoc Le. We also thank the Google Research, Brain Team and the open source contributors.

 Read how the power of AI and edge computing is critical to driving operational efficiencies and productivity gains.
Read how the power of AI and edge computing is critical to driving operational efficiencies and productivity gains.




 A new study creates a deep convolutional neural network using global satellite imagery to detect sustainable roofscapes—a promising strategy for climate mitigation.
A new study creates a deep convolutional neural network using global satellite imagery to detect sustainable roofscapes—a promising strategy for climate mitigation.