 NVIDIA Developer Program provides access to integrated technologies for simulation and real time rendering with Omniverse.
NVIDIA Developer Program provides access to integrated technologies for simulation and real time rendering with Omniverse.
NVIDIA Developer Program is now bringing NVIDIA Omniverse to over 2.5 million developers around the world. At SIGGRAPH, we’re introducing exclusive events, sessions, and other resources to unveil Omniverse as our newest platform for developers.
NVIDIA is delivering a suite of Omniverse apps and tools to enhance developer pipelines. Developers can plug into any layer of the platform stack — whether at the top level, utilizing prebuilt Omniverse apps; or the platform component level, so they can easily build custom extensions and tools to boost workflows.
With the NVIDIA Developer Program, Omniverse users have access to a wide range of technical resources, tutorials and more. From online training to interacting with the community, these developer resources are free, providing users with the tools and knowledge to familiarize themselves with the Omniverse platform.
Learn about all the different ways developers can engage with us at SIGGRAPH and dive into the Omniverse platform.
Get Access to the New NVIDIA Omniverse User Group
Join NVIDIA Omniverse for our inaugural User Group, an exclusive event hosted by Omniverse’s senior leadership on August 12, 5:00 – 6:30 p.m. PDT. The event is open to all developers, researchers, creators, students, hobbyists, and other professionals using the platform, will provide attendees with a chance to:
- Hear the vision and future of Omniverse from Rev Lebaredian, VP of Omniverse & Simulation Technology, and Richard Kerris, VP of Omniverse Developer Platform.
- Learn how you can build on and extend the Omniverse ecosystem.
- See the unveiling of the Create With Marbles: Marvelous Machines contest winners.
- Attend “Meet the Expert” breakout sessions and speak with engineering leaders about specific platform applications and features.
Register now to join this exclusive event.
Get Started With the Omniverse Developer Resource Center
The new NVIDIA Omniverse Resource Center has all the information needed to help Omniverse users get started and familiarize themselves with the platform. From talks and sessions to technical documentations, the Resource Center organizes all assets that are available for certain topics, making it easier for users to find overviews of different features and capabilities in Omniverse, including:
- Learning USD: Get an introduction to USD, from its creation to current implementation in Omniverse.
- Using Connectors: Learn how to connect your application to the Omniverse platform and submit your Connector for exposure to Omniverse users.
- Building apps and extensions: Use Omniverse Kit to build entirely new applications or add new functionality to the Omniverse ecosystem by creating extensions.
- Building microservices: Enable new capabilities to be exposed as microservices to any connected clients and applications.
For more resources, check out our developer tutorials.
New Graphics and Simulation Courses by NVIDIA Deep Learning Institute (DLI)
The NVIDIA Deep Learning Institute (DLI) offers resources for diverse learning needs—from learning materials to self-paced and live training taught by NVIDIA-certified instructors, to teaching kits for educators—giving individuals, teams, and institutions what they need to advance their knowledge in AI, graphics, and simulation.
Attendees can learn more about these free trainings and resources, including:
- Universal Scene Description (USD) for collaborative 3D workflows. This free, self-paced course provides an introduction to USD and important concepts like layer composition, references, and variants and includes hands-on exercises with live scripted examples.
- The new “Masterclass by the Masters” video series for artists to see how others are using and building on Omniverse. The first masterclass collection is “Using Omniverse for Artistic 3D Workflows,” which highlights how different creators are using the platform for multi-app design workflows.
- The Graphics & Omniverse Teaching Kit, which includes downloadable teaching materials and online courses that provide the foundation for understanding and building hands-on expertise in graphics and Omniverse. Educators can request early access.
Learn more about NVIDIA DLI.
Engage With the Community
NVIDIA hosts deep dives with developers on Omniverse applications such as Omniverse Create, Issac Sim Machinima, and more. We routinely invite product managers and community experts to present the latest features and most popular workflows. Doing this live on Twitch gives you a chance to ask questions in an interactive environment. Follow our Twitch channel for the schedule of upcoming streams and look at past events in our Community Stream playlist.
For additional support, check out the Omniverse forums and join our Discord server to chat with the community.

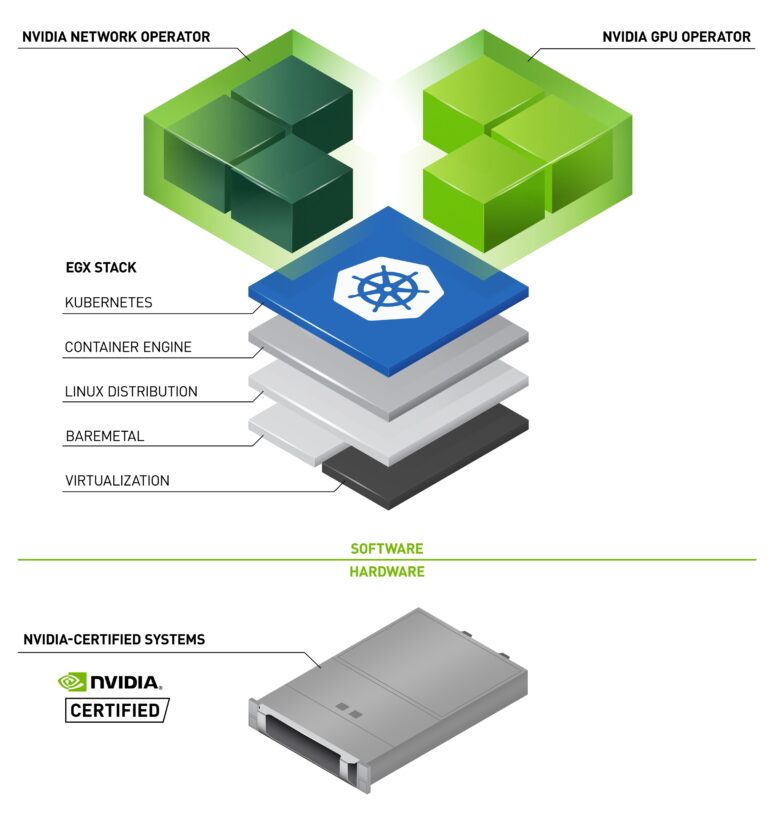 In the last post, we looked at how the GPU Operator has evolved, adding a rich feature set to handle GPU discovery, support for the new Multi-Instance GPU (MIG) capability of the NVIDIA Ampere Architecture, vGPU, and certification for use with Red Hat OpenShift. In this post, we look at the new features added in …
In the last post, we looked at how the GPU Operator has evolved, adding a rich feature set to handle GPU discovery, support for the new Multi-Instance GPU (MIG) capability of the NVIDIA Ampere Architecture, vGPU, and certification for use with Red Hat OpenShift. In this post, we look at the new features added in …  NVIDIA Developer Program provides access to integrated technologies for simulation and real time rendering with Omniverse.
NVIDIA Developer Program provides access to integrated technologies for simulation and real time rendering with Omniverse. In the SIGGRAPH Special Address, NVIDIA revealed that the upcoming release of Blender 3.0 includes USD support.
In the SIGGRAPH Special Address, NVIDIA revealed that the upcoming release of Blender 3.0 includes USD support. 